
This blog has a modern version at http://blog.tanyakhovanova.com/, where you can leave comments. This page contains the copies of recent blog entries. The older copies are here:
My goal is to expand my students' minds. So, though my STEP program is about mathematics, I sometimes give problems from other areas for homework. Here is a recent physics one.
Puzzle. You have a brick of 1 kilogram. How does the weight of the brick change during the year?
As always, my students generated tons of ideas about what can influence the weight.
I am not into physics. So, when I got these replies, I contacted a real physicist friend, Levy Ulanovsky. He referred me to Wikipedia: The first operational definition of weight was given by Euclid, who defined weight as: "the heaviness or lightness of one thing, compared to another, as measured by a balance." This implies that when we talk of "weight", we need to specify how we measure it. He continued by saying that the above ideas all make sense if we measure the weight force, e.g., by using a spring or pendulum frequency. Yet if our measurement is relative, e.g., by using a lever-like scale, then, for example, the sun's gravitational pull is not a valid answer.
For example, if we measure the weight using a lever-like scale, with our brick on one side and a known weight combination on the other, then the weight reading on the moon will be the same as on Earth. If you use a spring, the weight will be different.
He added: People often use the words "weight" and "mass" interchangeably. But for teaching, you may wish to clarify that weight force is mg. A change in pendulum frequency shows a change in g, the acceleration due to gravity. A balance (lever-like) can show a change in m, the mass on one of its two plates relative to the mass on the other plate, with g equal at both ends. A spring, a rubber band, or a springboard can show a change in the weight force mg, whether caused by a change in m, in g, or in both m and g. Of the four student answers, the moon and sun change g; weathering and moisture change m; thermal expansion has several effects that interplay in a complicated way, so we're better off forgetting about it.
I also asked Levy which effect is the strongest. His reply was: assuming a spring, a pendulum, or the like, the strongest effect is due to the Moon.
Here is a probability puzzle I heard from my son Sergei. We even included this puzzle in our book Mathematical Puzzles and Curiosities. Our book includes the answer but omits the details. So, this blog post is devoted to said details.
Puzzle. Alice rolls a die until she gets 6. Then Bob observes that she never rolled a 5.
Question. What is the expected number of times that Alice rolled the die?
The answer depends on Bob's strategy. Many people assume that Bob loves 5 and is only looking for 5. In this case, the answer is 3. Here is the argument: the expected number of rolls to get 5 or 6 is 3: this is equivalent to rolling a three-sided die and waiting to one side to appear. Only on the rolls without 5 will Bob say something.
However, there are other natural assumptions. In the book, we have two suggestions, where Bob treats every digit that is not 6 equally.
Modeling assumption 1. Suppose Bob lists all the numbers that are missing. Then, when he says that 5 is missing, we are guaranteed that Alice rolled 1, 2, 3, and 4 before 6. Such a strategy by Bob noticeably increases the expected number of rolls, and the answer is 8.7. Let us prove this.
This version of the problem is related to the coupon collector's problem. Suppose we randomly get coupons, where the total number of coupons is 5, and we get each one with probability 1/5. How many coupons will we need to collect to get 4 different coupons? The first coupon appears immediately after one draw; after that, a different coupon appears with probability 4/5, which means the expected additional wait is 5/4. After we get the second coupon, the expected wait for the third coupon is 5/3. Continuing, the total wait for four different coupons to appear is 5/5 + 5/4 + 5/3 + 5/2 = 77/12.
However, we actually need 4 different coupons, not out of 5, but out of 6 to appear. That means that we need to multiply the answer by 6/5 to get 7.7. Then we add one extra roll for the final 6. The answer is 8.7.
Modeling assumption 2. Suppose Bob randomly chooses one number out of the ones that are missing. For example, if Alice rolled 1, 2, 3, 2, 1, 6, then Bob notices that 4 and 5 are missing, and mentions 5 with probability 1/2. In this case, the number of expected rolls is 4.26.
By using coupon-collecting ideas, we know, for each k, the expected number of rolls until k+1 distinct dice faces appear. To wit, for each k=0,1,2,3,4, the expected number of rolls is 1, 2.2, 3.7, 5.7, and 8.7, respectively.
Now we need to condition on the event that Bob actually says 5. By symmetry among the non-6 faces, the probability that Bob's announcement is 5, given that he says something at all, is the same for each of the five digits. This conditioning does not bias the waiting time toward any particular missing digit, so the conditional distribution of the stopping time is obtained by averaging these expectations over the five possible values of k. Therefore, the expected number of rolls is (1 + 2.2 + 3.7 + 5.7 + 8.7)/5 = 4.26.
I am grateful to my other son, Alexey, for discussing this problem with me. Probability is a tricky subject, and it is nice to have experts in the family.
I wrote a book. This is my first book, so I am very proud. I wrote it together with two brilliant puzzle lovers, Ivo Fagundes David de Oliveira and Yogev Shpilman. The book is published by World Scientific and is available for pre-order: Mathematical Puzzles and Curiosities. Here is one sample puzzle from the book.
Puzzle. The centers of two opposite faces of a cube are connected by four distinct shortest paths, shown in the picture in different colors. Can you find two points on the surface of a cube such that there are exactly three shortest paths connecting them?

This puzzle appeared in the latest issue of SLMath's newsletter, 17 Gauss Way. The issue has a puzzle column that I coauthored with Joe Buhler and Pavlo Pylyavskyy. The coolest images in the column were done by Tracy Hicks, and this image is no exception. The picture is better than our original one in the book.
I recently gave my STEP students a question from our old 2014 PRIMES entrance test.
Puzzle. John's secret number is between 1 and 216 inclusive, and you can ask him yes-or-no questions, but he may lie in response to one of the questions. Explain how to determine his number in 21 questions.
Here is the standard solution. We start by asking John to convert his number into binary and add zeros at the beginning if needed to make the result a binary string of length 16. For the first 15 questions, we do the following. For question i, we ask: "Is the i-th digit of your string zero?" For question 16, we ask, "Have you lied in response to a previous question?" If he lied on a previous question, he must say YES. If he didn't, he might lie on question 16 and also say YES. In any case, if the answer is NO, he didn't lie on the first 15 questions and we know the first 15 digits of the number. Then, we ask about the last digit three times, and the answer given at least twice is correct, so we know the number.
If the answer to question 16 is YES, then he lied on one of the questions 1–16. From now on, he has to tell the truth since he already lied. We use binary search (4 questions) to determine on which question he lied. This will tell us the first 15 digits, and we can use the 21st question to find the last digit.
One of my students, Tanish, invented an out-of-the-box solution that uses 18 questions. The idea is to force John to lie in the first two questions, and then safely proceed with the binary search.
He suggested asking the following two questions: "Are you going to answer NO in response to the next question?" and "Did you respond YES to the previous question?" The reader can check that whatever John replies, he is forced to lie exactly once.
Another student, Vivek, had a similar idea but used only one question to force John to lie: "Will you say NO to this question?"
My team, Death and Mayhem, organized the 2025 MIT Mystery Hunt. The hunt was a great success. Many people commented that it was the best mystery hunt ever.
This year, we added a new and interesting feature. Not only were teams allowed to choose which puzzles to unlock, but they were also given a short description of each puzzle in addition to its title. So, small teams who liked crosswords could choose to work only on crosswords.
As usual, I will list the mathy puzzles, including our official puzzle descriptions. All the puzzles can be found at the hunt's All puzzles page.
We had a special round called Stakeout, with easy puzzles. My team isn't too nerdy, so we didn't have too many mathematical puzzles overall, and just two puzzles with a math flavor in the Stakeout round, incidentally coauthored by me. Somehow, I like designing easy puzzles. There were two additional puzzles in this round that I enjoyed during testing. I loved the popsicle puzzle so much that I brought it to my grandchildren to solve.
The first round wasn't too difficult either. Several people praised the ChatGPT puzzle, though it's not mathy.
Now, moving to more difficult puzzles, Denis Auroux is famous for designing fantastic logic puzzles. His puzzles below aren't easy, but many people loved them. I even heard magnificent as praise.
Here are two puzzles I test-solved and enjoyed. The first one is a logic puzzle, while the second one isn't math-related.
Here are two puzzles that I edited and highly recommend. The first puzzle was initially called Gin and Tonic; I wonder if anyone can guess why.
These are math-related puzzles that people liked.
I asked only a few people for recommendations. These are math-related puzzles that weren't mentioned but seem cool. The fourth puzzle was an invitation to the Mystery Hunt, which, not surprisingly, was a puzzle.
I also got a recommendation for a non-math puzzle, which I would definitely have enjoyed watching solved. I'm not sure I'd enjoy solving it alone.
Finally, here is the list of non-math puzzles that seem cool. A warning about the first puzzle: It's rated R. The first three puzzles are relatively easy; they are from the Stakeout round.
Here is a video from Cracking the Cryptic, joined in this episode by Matt Parker, titled Matt Parker Sets Us A Challenge!. The video is devoted to the second part of the puzzle Maze of Lies, mentioned above, by Denis Auroux and Becca Chang.
Take a look at a card one of my students gave me last December. You can spot the Koch snowflake, the Sierpiński triangle, and the Sierpiński carpet on it. I guess my fractal class was a hit.
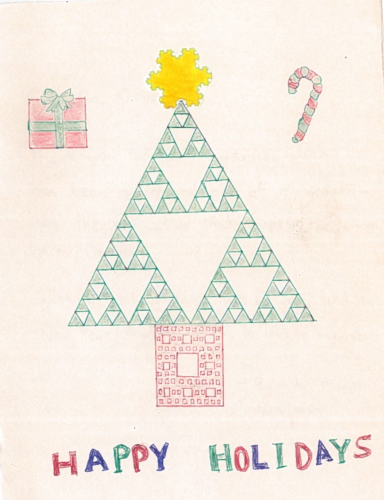
I am a proud member of the Death and Mayhem team, which participates in the MIT Mystery Hunt every year. This year, our team had the honor of running the hunt.
Here is a puzzle I contributed, titled A Math Quiz. It consists of a list of math problems. I am especially happy that I was able to turn a collection of cute math puzzles into a puzzle-hunt challenge with a word or phrase as its final answer.
Imagine you're watching a magician. She pulls out two perfectly ordinary boxes — or so it seems. One box is inside the other, like a set of nesting dolls. So far, nothing suspicious.
Then she removes the smaller box, closes the larger one, and slides the larger box inside the smaller one. Ta-da!
The name comes from the way one box goes into the other. Would you like to know the secret? The two boxes are actually identical. Moreover, they are not cubes but cuboids. The inner box is fully closed, while the outerbox is slightly expanded, and the inner box is rotated relative to the outer one.
I first heard about Gozinta Boxes at the Gathering for Gardner conference in 2024. Ivo David gave a talk and presented his new trick: Triple Gozinta Boxes, which you can now buy at TCC Magic. He can place three boxes inside one another — and then repeat the trick in the reverse order.
During his presentation, David mentioned that he knew how to prove that you cannot have more than ten Gozinta Boxes. My immediate reaction was that ten must be overkill. So I decided to give the problem to my STEP students as a project.
We proved that in three or higher dimensions, the maximum number of boxes is three. We also showed that in two dimensions, the maximum is four. You can find all the details in our paper Mathematics of Gozinta Boxes, posted on the arXiv. But we didn't stop there. We invented a new trick. We constructed three boxes such that not only can they be nested in one order — say, ABC — and in the reverse order, CBA, but they can also be nested in three additional orders, for example ACB, BAC, and BCA. We also proved that achieving all six possible orders is impossible. You can see the trick in the video below or by following the link for A New Gozinta Boxes Trick.
I met Alexander Karabegov during the All-Soviet Math Olympiad in Yerevan. He was one year older than me. By then, when I was still competing in 1976, he was already a freshman at Moscow State University. He proposed the following two related puzzles for the Moscow Olympiad, which I had to solve.
Puzzle 1. You are given a finite number of points on a plane. Prove that there exists a point with not more than 3 closest neighbors.
Just in case, by closest neighbors I mean all points at the minimal distance from a given point. I am sure I solved both puzzles at the time. I leave the solution to the first one to the reader.
Puzzle 2. Can you place a finite number of points on the plane in such a way that each point has exactly 3 closest neighbors?
The last problem has an elegant solution with 24 points chosen from a triangular grid. The story continued almost 40 years later, when Alexander sent me an image (below) of such a configuration with 16 points. He conjectures that this is the minimal configuration.

Karabegov's Conjecture. Any finite planar point configuration in which every point has exactly 3 closest neighbors must contain at least 16 points.
Can you prove it?
Initially, I didn't want to give the 24-points solution, but the image above is a big hint, so here you go.

Both constructions reveal the same underlying pattern. The constructions consist of rhombuses formed by two equilateral triangles, and the rhombuses are connected to each other. The 24-point construction consists of 6 rhombuses, while the 16-point construction consists of 4 rhombuses. What will happen if we try the construction with 3 rhombuses? The image below shows such a configuration, which now has extra edges with the shortest distance. We now see 3 points with more than three closest neighbors each, violating the condition. So the conjecture doesn't break.

So far, every smaller attempt failed — can you prove that 16 is minimal?
I was teaching my students the Knaster method of dividing an estate, which I learned from my friend Ingrid Daubechies. Let's look at an example.
Problem. Alice and Bob are divorcing. They have the portrait of Alice's grandpa and $10,000. Alice values the portrait at $10,000 because of its sentimental value. Bob values it at a market price of $2,000. How do they divide their estate?
Here is what my students initially suggest.
Let's look at these suggestions in greater detail. Alice values the whole estate at $20,000; Bob values it at $12,000. In the first version, Alice gets half of the estate from her point of view; Bob gets the rest, which is more than half in his point of view. The students are obviously rooting for Bob. In the second version, Bob gets half of the estate in his estimate, while Alice gets the rest, which is more than half in her estimate. The students are obviously rooting for Alice. After some discussion, the students agree that there should be a number between $5,000 and $10,000 that Bob gets, which would be a fairer division than the two initial examples. But how do we find such a number?
This is where the Knaster algorithm comes in. The main idea is that each gets the same amount of money on top of their perceived half. In other words, the Knaster method treats the estate like a sealed-bid auction and equalizes bonuses. Alice thinks that her fair half is $10,000, while Bob thinks his half is $6,000. To equalize bonuses, we want Alice and Bob to each receive their perceived half plus the same amount — call it x. Solving gives x = $2,000. Alice gets the portrait and $2,000, while Bob gets $8,000.
This is a beautiful algorithm that allows each person to be very happy, receiving more than one half. The bigger the taste difference, the more each person gets on top of their portion. The next question is: how can people cheat if they know this algorithm is used?
Alice can cheat by claiming that she values the portrait at $2,000 plus epsilon. Epsilon is needed to guarantee she gets the portrait. This way, they both value the estate the same. Alice gets the portrait and $4,000, which is $2,000 more than the honest way. Symmetrically, Bob can cheat by claiming he values the portrait at $10,000 minus epsilon. This way, he gets $10,000, which is $2,000 more than the honest way.
I've been teaching this topic several times now. This year, my student Ben had an out-of-the-box idea on how Alice can cheat. Alice declares that she values the portrait at $0. Bob thinks the estate is worth $12,000, while Alice pretends that she values it at $10,000. After the calculation, Bob gets the portrait and $4,500, which is $500 more than his half of the estate in his view. Alice gets $5,500, which is $500 more than half of the estate in her declaration. Then she buys the portrait from Bob for $2,000. In the end, Alice gets the portrait and $3,500, way more than she would get after an honest use of the algorithm.
The first cheating method seems more profitable than the new one. But still, I love it when my students suggest unexpected ideas.
Recently, I gave my STEP students the following discussion question.
Puzzle. A long time ago, before anyone had ever heard of ultrasound, there was a psychic who could predict the gender of a future child. No one ever filed a complaint against her. Why?
I based this puzzle on a story I once read. In the story, the psychic kept a neat little journal where she wrote down each client's name and the predicted gender — except she secretly wrote down the opposite of what she told them. When someone came back complaining that she was wrong, she would calmly open her journal and say, "Oh, you must have misheard".
This scam demonstrates conditional probability. The satisfied customers never came back; only the unhappy ones did — and those she could 'prove' wrong. Understanding probability can help my students detect and expose scams.
My students, of course, had their own theories. The most mathematical one was a pay-on-delivery scheme: if the psychic was right, she got paid; if not, she didn't. Another innocent idea was for the psychic to keep moving. By the time the babies were born, she'd be long gone predicting future children's genders somewhere far away.
ChatGPT offered a different explanation: the psychic never said whose future child she was predicting. If the prediction failed, she could always clarify that she meant someone else's child. After some prodding, the idea evolved and became even sneakier: If the prediction failed, she could always clarify that she meant the couple's next child, or, if they weren't planning more children, a grandchild. Another brilliant, but unrealistic idea was to never charge anyone. Hard to sue someone who never took your money.
One student suggested that the psychic wasn't wrong at all — she was predicting the baby's true inner gender. In today's world, rather than in the world before ultrasound, that one almost sounds plausible!
And finally, I'll leave you to guess one more explanation — proposed, surprisingly, by several students. (Hint: they were disturbingly creative.)
To conclude: I enjoy teaching my students. Understanding probability won't let them predict the future, but it might make them less gullible.
Once I wrote a blog essay titled Seven, Ace, Queen, Two, Eight, Three, Jack, Four, Nine, Five, King, Six, Ten. It was about a "magic" card trick.
If you want to perform this trick with one suit, the title of that earlier post tells you exactly how to stack your deck.
In the fall of 2023, I gave this trick as a homework problem to my STEP students. The result? We ended up writing a 40-page paper, Card Dealing Math, now available on the arXiv. At one point, we seriously considered calling it The Art of the Deal, but decided against it.
In the homework version, the deck consisted of cards from a single suit, but we generalized it to a deck of N cards labeled 1 through N. The dealing process we studied is called under–down dealing: you alternate between placing one card under the deck and then dealing the next one face-up. It's very similar to down–under dealing, where you start by dealing the first card instead. These two patterns are often, unsurprisingly, called the Australian dealings.
The under-down dealing turns out to be mathematically equivalent to the Josephus problem. In that famous ancient problem, people are arranged in a circle, and you repeatedly skip one person and execute the next (much grimmer than playing with cards). The classic question asks: given N people, who survives? In our card context, this corresponds to asking where the card labeled N ends up in the prepared deck.
More generally, the Josephus problem can ask the following question. If we number the people in a circle 1 through N, in what order are they eliminated? In our research, we flipped the question around: how should we number the people in the circle so that they're eliminated in increasing order?
Naturally, we couldn't stop there. We explored several other dealing patterns, discovered delightful mathematical properties, and along the way added 44 new sequences to the OEIS. The funnest part? We also invented a few brand-new card tricks.
Puzzle. How can you make the following equation correct without changing it: 8 + 8 = 91?
The intended answer: turn the paper over! When flipped upside down, the equation becomes 16 = 8 + 8.
As you might expect, my blog post doesn't stop there. I'd like to share some creative ideas my students came up with when they tackled this puzzle as part of their homework.
The most common suggestion was to interpret the equation modulo some number. For example, it works modulo 75. By extension, it also works modulo any divisor of 75: 3, 5, 15, or 25.
They also suggested interpreting the equation in base 5/3.
One far-fetched but imaginative submission proposed the following: Suppose the equation is written in an alien language whose symbols look identical to ours but have different meanings. In this alien base-10 system, the symbols + and = mean the same as on Earth, but an 8 represents 6, a 9 represents 1, and a 1 represents 2. Then the alien equation 8 + 8 = 91 translates to 6 + 6 = 12 in human, which is perfectly true.
But my favorite answer was the following:
The title sounds like a list of healthy foods. However, this list is from the homework I gave to my students.
Puzzle. Which one doesn't belong: egg, banana, apple, walnut, tangerine, or avocado?
The book answer was apple as the only one which we can eat without peeling.
Other students suggested a lot of reasons why egg is the odd one out.
Overall, the students found reasons for each of them. In addition to the above, we have the following.
I start my homework with warm-up puzzles.
Puzzle. Two friends went for a walk and found $20. How much money would they have found if there were four of them?
The answer, of course, is $20. The number of people doesn't change the amount of money lying around. Even ChatGPT gave this answer. Duh!
My hope was to catch them not paying attention and mindlessly multiply to get $40.
To my surprise, some of them answered $80. The 'them' in the problem is not specified. It appears that they read the puzzle as if they found one 20-dollar bill, and them was referring to bills.
One student wrote a thoughtful reply: Having more friends most likely wouldn't change the amount of money found, considering the amount of money is independent of the number of people, meaning the friends would still find $20. However, with double the people, they may find more money in other locations. There is also a chance that the 2 extra friends would make the group walk a different path, meaning they wouldn't find money at all.
I recently posted the following puzzle about identical triplets.
Puzzle. Three brothers who are identical triplets live on the seventh, eighth, and ninth floors of the same apartment building. Their apartments are identical and vertically stacked. One day, all three step onto their balconies, standing in the same upright posture. The brother on the eighth floor shouts, "AAAA!" Which of the other two will hear him first?
Most readers got it right: our mouths sit lower than our ears. That means the distance from the mouth of the brother on the eighth floor to the ears of the brother on the seventh floor is shorter than the distance to the ears of the brother on the ninth floor. So the seventh-floor brother hears it first.
However, one reader, Ivan, taught me something I didn't know: identical twins aren't always identical. He even sent a photo of Mark and Scott Kelly — identical twins of different heights.
Of course, as a first approximation, we can assume identical triplets are identical. But mathematicians are nitpicky and like precision. Ivan (clearly a mathematician at heart) also noted that even identical twins might wear shoes with different heel heights, which could tweak the distances.
Here's another reader submission that made me smile:
Nitpicking again: that's a stretch, since the problem says they're standing — but it's still funny.
Here's a problem from our 2025 STEP entrance test, taken by nearly a hundred students.
Problem. Pavel likes pets. All his pets except two are dogs. All his pets except two are cats. All his pets except two are parrots. The rest of the pets are cockroaches. How many pets of each kind does Pavel have?
Here is a solution from one student: one cat, one dog, and one parrot. No cockroaches—phew. Most students (and ChatGPT) found this one. By the way, I ran my whole test through ChatGPT, and this was the only mistake it made. ChatGPT, along with many students, missed the second solution: Pavel has two cockroaches.
Two more students' answers made me smile:

When I graduated high school, I got a special certificate I was absurdly proud of. It wasn't about grades — students voted for these, supposedly to honor strength of character. The award was called the Pledge of Honor.
When you open it, the left-hand side has a quote attributed to Friedrich Engels: "A human is defined not only by what he does, but also by how he does it."
I couldn't find the official translation of this quote, so the above translation is my own. While I was searching, I found another quote: "The less you eat, drink, and read books, the less you have to shit, pee, and talk." But I digress.
Before I explain what's on the right-hand side of the award, a little context. I was a member of Komsomol, the Leninist Young Communist League in the Soviet Union. About 99% of students were members — not because of boundless zeal, but because not joining could hurt your chances of getting into college or landing a job. Back in high school, I was brainwashed into believing that the Komsomol was trying to do good, so I signed up as soon as I was eligible — I wasn't thinking then about colleges or jobs.
Now I am ready to translate the right-hand side, which said: "The Komsomol organization of Moscow School No. 444 PLEDGES ON ITS HONOR that Tanya Khovanova will never, ever, anywhere disgrace the high calling of a Komsomol member."
I lost my rose-colored glasses right after high school. How that happened is another story, but let's just say the "never, ever" promise had a shelf life of about a month.
There was another, more prestigious certificate called the Torch-Carrier of Communism. Two students in my class received this honor. One of the torches soon moved to Israel.
Here's a neat coin puzzle I received by email from my reader s_hskz2 (at twitter.com).
Puzzle. You have 9 coins: 3 gold coins, 3 silver coins, and 3 bronze coins. Within each metal, the coins are indistinguishable. Exactly one gold, one silver, and one bronze coin are counterfeit; the other six are genuine. You are provided with a magic bag that functions as follows: when you place a subset of coins into the bag and cast a spell, the bag glows if and only if the subset contains all three counterfeit coins. Can you identify all three counterfeit coins using at most 5 tests?
I tried to find an easy solution and didn't. Then I decided to use information theory to guide me to an answer. Unsurprisingly, it worked. The solution wasn't trivial, but it was a lovely practice in using information theory for such puzzles.
Later, s_hskz2 sent me a more difficult version: There are 10 coins of each kind, and you are allowed to test 10 times, but I was too lazy to try.
Puzzle. Three brothers who are identical triplets live on the seventh, eighth, and ninth floors of the same apartment building. Their apartments are identical and vertically stacked. One day all three step onto their balconies, standing in the same upright posture. The brother on the eighth floor shouts "AAAA!" Which of the other two will hear him first?
I gave this puzzle to my students, and two of them offered the right answer for the wrong reasons. One said, "The seventh-floor brother, because air is warmer closer to the ground and sound travels faster in warmer air." Another said, "The seventh-floor brother, because the air is denser at lower altitude and sound travels faster in denser air."
What is the right reason?
For the last homework assignment, I gave my students the task of finishing a famous Russian joke.
The joke was that the Russian newspapers truthfully reported that the Russian car came in second and the American car second to last.
One of my students, William, got a different idea and wrote a whole article.
AMERICAN CAR STOPS RUNNING LONG BEFORE RUSSIAN CAR FINISHES RACE
A Russian car and an American car were competing in a two-car race. At one point, the American car mysteriously drove off the race course and stopped. Of course, this meant that the race was over for them. All that the Americans could do was watch on the sidelines for the Russian car to reach the end of the course, which it completed successfully. The outcome of the race was in no way uncertain. Congratulations, Russians!
We recently wrote a blog post on how to generalize the game of SET and promised to continue. Here we are. But first, a reminder of what the game of SET is.
In the game of SET, we have 81 cards, each containing one, two, or three of the same object. The object is green, red, or purple, the shape is squiggly, oval, or diamond, and the shading is empty, full, or stripped. Three cards form a set if, for every feature, the attributes are all the same or all different. An example of a set with all features different is shown below. By the way, such sets are usually more difficult to spot. In the game, you need to find sets as fast as you can.

If we assign each attribute value a number 0, 1, or 2, we get an equivalent definition of a set. Three cards form a set if and only if the values for each feature sum to zero modulo 3. Thus, we can see our cards as vectors in the space F34. Three vectors form a set if they sum up to 0.
The generalizations we described in the previous post, were the following. We pick a different group and define a set as a few cards that might need to be in a specific order that multiply to the group's identity.
However, there is a different way to generalize sets to groups. Three cards that form a set in a classical game of SET, taken in any order, form an arithmetic progression. In other words, if a, b, and c form a set, then vectors b−a and c−b are the same. We can check this. We have c−b = c−(c+b+a)−b =−2b−a = b−a.
Thus, we can generalize the game of SET differently. Suppose cards are vectors in some space. We say three of them, a, b, and c, form a set if and only if b−a = c−b. Now, the order becomes important, similar to our previous generalization. We do not need to use commutative groups like vector spaces. For any group, our condition is equivalent to ba-1 = cb-1. Thus, c = ba-1b.
Interestingly, we do not care much about the identity card, meaning the card deck is a torsor. We introduced the notion of a torsor before, which informally is a group that forgets about its identity. Now, let's check possible examples.
Suppose the values of one attribute correspond to Z4. This game is not very inspiring as two values, a=0 and b=2, can be completed to a set with the third card, which equals c=(0,0,0) and is already used. The next interesting example is Z5. Here, values a=0 and b=2 can be completed to a third value c=4. We will leave it to the reader to check that for any two cards, a and b, the third card, c, differs from both a and b.
To make it more visual, we can use a pentagon with one marked direction. We fix the pentagon in space. In this case, three cards form a set if and only if the directions of the first and the third card are symmetric with respect to the direction of the second card. If we want to use three pentagons, we can reuse the cards from the game C53T, we described in our previous post. To make this game more visual, we can use three pentagons. We can mark each coordinate with a direction on the corresponding pentagon. The colors are to allow players to visually process the cards faster. For theoretical purposes, the colors can be ignored. Also, the pentagons themselves have different intensities of gray to emphasize that the game is played on each of them separately and also help choose the top of the card.

Let us go back and calculate when it is possible that the element that completes a set is already used. If our initial elements are a and b, then we need ba-1b to complete a set. If this element is equal to b, then a = b, which contradicts the assumption that we start with two different cards. Suppose ba-1b = a, then, equivalently (ba-1)2 = 1. The new element can be the one that is already used if and only if the group contains elements of order 2.
Can we use other decks we described in the previous post? Consider the game ProSet/Socks. The group is commutative, and every element is of order 2, which means ba-1b is always a. We can't use the deck at all! What about the EvenQuads deck? It can be viewed as Z43, so it is possible that we can't complete any two cards to a set. However, there is a bigger problem with the deck. To play with it, we need to actually assign values to colors and shapes. We are saying that even if we decide to use the group, we should make different cards! For example, we can style the cards as squares like the pentagons above.
We also mentioned in the previous post the group, which is the wreath product of S2 and S3. Consider the following example of two cards that were screen-printed from the Numberphile video on the variations of the game of SET.


The first card, a, is the inverse of itself, so the third card we are looking for is described as the product bab, which we can visualize as the following. If we ignore the beads, the card that completes the set is a. Luckily, if we do not ignore the beads, it is not a; we need to add two beads to a.



The product of permutations is difficult to visualize, so playing this game with the cards in the Numberphile video might be difficult. The good news is that this group can be visualized in many different ways:
We want to show you a beautiful deck from the tsetse website that allows you to use any one of the four definitions to play the game. The game is called OCTA Set, as the underlying group is called an octahedral group. An example of a set is in the image below, where the top and bottom shapes represent the same element of the group. Moreover, the deck is a torsor: there is no the identity card.

Let us prove that this is a set. Consider the bottom cube shape. Comparing the first two cards, the top face doesn't change. We can see that the symmetry of the cube is the 90-degree clockwise rotation around the line that goes through the centers of green faces. In such a rotation, the left face on the second card keeps the color from the first card, while the right face takes the color from the left face on the first card and swaps hollowness. We see that the third cube completes the set.
For another proof, let us look at the top shape and discuss what happens with the permutation of colors when changing from the first card to the second. The left color moves to the bottom, the bottom color to the right, the right color to the center, and the center color to the left. Not surprisingly, we got a cyclic permutation of order 4, similar to a 90-degree rotation being of order 4. The same thing happens when moving from the left to the right. The swirl stays the same.
As we mentioned, when you play this game and pick two cards then calculate what card completes the set, you might discover that it is one of the cards you picked. The probability that two cards in a specific order can't be completed into a set is the same as the probability of picking a random element in our group and discovering that it has order 2. The symmetric group S4 has 9 elements of order 2. Thus, the direct product with S2 has 19 elements of order 2, giving a probability of 19/48. For completeness, this group also has 8 elements of order 3, 12 elements of order 4, 8 elements of order 6, not to mention the identity of order 1.
If ba-1 is an element of order three, then the cards a, b, and the card c that completes the set form a set when they are taken in any order. As a tradition in mathematical writing, we leave it to the reader to check that fact. Just a reminder that in the game of SET, the group element ba-1 always has order 3.
Notably, there was nothing special or extraordinary about the group discussed above. It has a pretty visualization as a cube or octahedron, but is not otherwise particularly interesting. The reason why this group allowed for these two platonic solids to be used to visualize it is because the cube is dual to the octahedron. But we could have similarly used any group to play set! One such example might consider using the group of symmetries of the other pair of dual platonic solids, the icosahedron and the dodecahedron. This group is actually equivalent to A5, also known as the alternating group of order 5, which consists of all even permutations of five elements. The tsetse website we mentioned above contains an implementation of such a game called A5SET (pronounced "asset"). The design of the site, games, and cards was done by Andrew Tockman and Della Hendrickson.
The world is full of groups and symmetries. Any group can be turned into a game of SET!
Foams are cool mathematical objects studied by my brother, Mikhail Khovanov. I already wrote about them in my previous blog posts, Foams Made out of Felt and Tesseracts and Foams. Here, I would like to explain why foams are so cool, but first, I need to remind you of their definition. Foams are finite 2-dimensional CW-complexes, such that each point's neighborhood must be homeomorphic to one of the three objects below.
Foams are cool: they are 2-dimensional CW-complexes embedded in 3-space, with singularities only of the most generic kind, which makes them relatively simple. Moreover, they are combinatorially defined, which makes them easier to work with than with many other geometric objects.
My two previous blog posts have some pictures, but now, I just want to discuss a generic planar cross-section of a foam, which is a planar graph. In the cross-section, seams become vertices, and faces (regular points) become edges. The tripod condition above implies that the resulting graph is trivalent: each vertex has degree 3.
The most interesting foams are tricolarble: foams where their faces can be colored in three colors, so that each face has its own color, and, at the seams, three faces of three different colors meet. The cross-section of such a foam makes a tricolorable trivalent graph. This coloring is called Tait coloring. The cool thing is the Tait's theorem connects the Tait coloring to the 4-color theorem.
Tait's theorem. The following two statements are equivalent.
- Every planar graph is 4-colorable.
- The edges of every planar bridgeless trivalent graph are 3-colorable.
I won't discuss the proof here, but I will explain how to color the edges of a graph in three colors when the faces are colored in four, and vice versa.
Assume that the four colors of the faces form a group of four elements, called the Klein group. Let's say that gray is the identity, and red, blue, and green are the rest. Then, the product of gray and x is x. The product of any two non-gray colors is the third non-gray color.
Given a trivalent graph G whose edges are colored in three colors, we can color the faces of that graph in the following manner. Color one of the faces a random color. Then, calculate the colors of the other faces so that each edge's color is the product of the colors of neighboring faces.
Going back, if we have a planar trivalent graph with faces colored in four colors, we can assign an edge a color that is the product of the colors of neighboring faces. As neighboring faces have different colors, the product of those colors is never gray (the identity). Thus, the edges will be colored in three colors. I leave it to the reader to check that three edges incident to a vertex must be colored in different colors.
Kronheimer-Mrowka homology theory of graphs states that the Kronheimer-Mrowka homology of a trivalent graph is non-zero if and only if the graph has no bridge. If one can prove that the rank of the homology group is the number of 3-colorings of the edges (or at least that the non-zero homology implies the existence of the tricoloring of that graph), then the Four-color theorem would follow from Tait's theorem.
Foams are cool by themselves, but there is hope that they might provide a conceptual proof of the Four-color theorem, making them awesome!
Do you know that 2025 is a composite, deficient, evil, odd, square, and powerful number? I collect properties of numbers at my Number Gossip website, where you can also find detailed definitions of these terms. Provocatively, 2025 is also an apocalyptic power, meaning that 2 to the power of 2025 contains 666 as a substring.
Recently, Tamas Fleischer sent me an email discussing additional fascinating properties of 2025. While I am slowly deciding whether to add them to my database, there is some urgency in posting these properties in anticipation of the coming year. Here's the material from Tamas, retold in my own words.
Out of the properties mentioned earlier, the square property is the only rare one. On my website, I define a property as rare if fewer than 100 numbers below 10,000 possess it. Square numbers barely make the cut. But 2025 is not just a square number—it is the square of a triangular number. If you remember the formula for the sum of cubes of the first n natural numbers, the result is (n(n+1)/2)2, which is the square of the nth triangular number. Thus, 2025 is the sum of the cubes of all one-digit numbers.
Additionally, 2025 is the product of 25 and 81. My website notes an intriguing property shared by 25 and 2025: both remain square numbers when all their digits are incremented by 1. For example, 25 becomes 36, and 2025 becomes 3136, both of which are squares. Moreover, 25 is the smallest such number, and 2025 is the second smallest. What my website does not mention is that their square roots exhibit a similar pattern. The square roots of 25 and 2025 are 5 and 45, respectively. When their digits are incremented by 1, the results are 6 and 56, the square roots of 36 and 3136, respectively. The original and incremented squares and their square roots are tied together in a surprising way.
2025 also shares an interesting property with 81. Both are square numbers with an even number of digits and if you split the digits in half and sum the halves, the result is the square root of the original number. For 81, splitting into 8 and 1 gives 8 + 1 = 9, which is the square root of 81. Similarly, for 2025, splitting into 20 and 25 gives 20 + 25 = 45, the square root of 2025. Intriguingly, 81 is the smallest number with this property, and 2025 is the second smallest.
Thank you, Tamas, and Happy New 2025 to everyone!
Once, I gave a puzzle to my students as homework just to check their level of attention.
Puzzle. A family has two identical twins. One of them is a boy, what is the probability that the other one is a boy?
What can I say? Some of the students didn't pay attention and gave weird answers like 1/2, 1/3, and 2/3.
The twins are IDENTICAL. The other one has to be a boy! Duh!
One of the students was well-educated and mentioned that it is theoretically possible for different twins to be different genders, though this is extremely rare. When one fertilized egg splits into two, producing two embryos, the genetic material of both eggs is the same, almost. Some errors during splitting are possible, and it seems that some very particular errors can lead to the identical twins being identified as a boy and a girl. I never knew that before!
However, one student thought outside the box. In his vision, a family adopted two identical twins who aren't each other's twins, just happen to be identical twins with someone else.
Here is a puzzle for middle school students from the Möbius tournament.
Puzzle. For which natural numbers n greater than 1 it is possible to arrange n numbers 1 through n in a circle so that the difference between two neighbors always divides n?
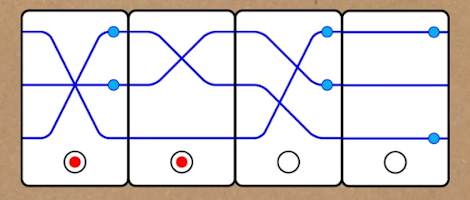
A new hat puzzle from Gribalko, reminding me of traffic lights.
Puzzle. You and six of your mathematician friends each have a hat placed on your head. Each of you can see the hats of all the others but cannot see your own. You were all told that there were three red, three yellow, and three green hats in total, but two of them were hidden. Your friends began to say the following phrases in sequence:Can you determine what color hat you have on your head?
- First: "I don't know what color my hat is."
- Second: "I also don't know what color my hat is."
- Third: "I also don't know what color my hat is."
- Fourth: "I know that my hat is red."
- Fifth: "But I still don't know what color my hat is."
- Sixth: "And I am sure that my hat is yellow."
I once saw a TikTok video featuring a puzzle: four matches were arranged to form a plus sign, and the challenge was to move one match to create a square. The solution shown differed from what first came to my mind, so I decided to share the puzzle with my students. Instead of drawing a diagram, I described it to them in words.
Puzzle. Arrange four matches to form a plus sign. Move one match to form a square.
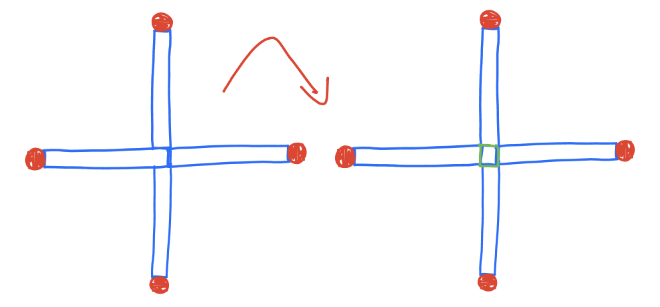
Most of my students gave the same solution shown in the video: moving one match slightly away from the center to create a square in the center, with the inner edges of the matches forming its borders. Not all the students were as lazy as I was; some drew pictures to illustrate. One example is shown below, where the resulting square is in green.
My solution, also discovered by a couple of students, was to move one match to form the number 4, which is a square.
I am glad I didn't provide a picture because it led to two unexpected solutions. For the first one, imagine a 3D shape out of four matches where one projection forms three sides of a square, and the other one is a plus sign. We can take the match from the plus sign that is not a side of a square and use it to complete the square. The second solution is shown below. The arrangement already contains a small square, so you can take a match and put it back. Being lazy brings benefits!
The deck for the game of SET consists of 81 cards. Each card has 1, 2, or 3 identical objects. Each object is an oval, a diamond, or a squiggly, colored in red, green, or purple, and the shading can be solid, striped, or empty. Three cards form a set if, for each feature (number, shape, color, shading), all three are either the same or all different. For example, one red striped squiggly, two red striped ovals, and three red striped diamonds form a set. The numbers are all different (1, 2, and 3); the shapes are all different (squiggly, oval, diamond); the color is the same (red), and the shading is the same (stripped). Another example of a set with all features different is shown in the picture.

For every feature, we can assign values of 0, 1, 2, modulo 3. The fact that the values are the same or all different is equivalent to saying that the values sum up to zero modulo 3. Thus, we can view the cards as points in a 4D vector space over the field F3, namely F34. Three cards form a set if and only if the corresponding vectors sum up to the zero vector. Sets have a very useful property: for any two cards in a deck, there exists a third card that completes the given two cards to a set.
Before we generalize the game of SET, let's talk about notation. Above, we looked at the values we assign for one feature as the field F3. If we want to talk about vectors, since technically a vector space must be over a field, we could use this definition. However we do not use its multiplicative properties, so we can say that values for one attribute are in Z3. If we want to forget about the exact values, and just use the group structure, we can use notation C3.
Let's see in what ways we can extend this definition. People have tried to generalize the game of SET to a group. Suppose each card corresponds to an element in a group. Then, we want to arrange three cards so that the corresponding three elements multiply to the identity. If the group is non-commutative, then the order matters. That means the players do not just pick out the three cards, they have to arrange them in a line so that the corresponding product is the identity. However, we still retain a useful property. If our card deck contains all possible elements of the group, then for any two cards in a given order, there exists a card that completes them to a set so that the product is the identity. However, another problem is that this card might be one of the cards we already have. On the plus side, we can rearrange the order of the cards, getting more options. We can also say that a set can consist of any number of cards, not just 3, as long as the product is the identity.
The Numberphile video The Game of Set (and some variations) shows examples of such games. One of the decks they show represents the group S3: permutations of 3 elements. The picture shows a screenshot from the video with a set in a different group, but if you ignore the blue beads, you will get a set in S3. The red dots at the bottom mark odd permutations. This helps see sets faster: each set has to have an even number of red dots. This deck is a toy example of what is possible with only 6 elements in the group.
They also show a similar deck corresponding to group S4: permutations of 4 elements. Thus, the deck size is 24. Despite the size not being very big, the video claims that the game is tough to play. One more deck represents two permutations of 3 elements, and one must get to the identity on both of them. Thus, the deck size is 36, and the underlying group is S32. These games are sometimes called Non-abelian sets. A third deck is a deck with three crossing lines with beads. The crossing lines correspond to permutations of three elements, and each string either has a bead or not. To get to the identity, you need an even number of beads on each line. Thus, the deck size is 48 and corresponds to the group that is called the wreath product of C2 and S3, where Cn is the cyclic group with n elements. The wreath product is used because a copy of C2, each of the beads, is associated with each of the three lines that the first group, S3, is acting on.
The screenshot from the video we mentioned corresponds to this group, showing four cards forming a set. The red dot at the bottom signals the parity of a permutation, and there has to be an even number of them, but you can ignore them. However, the meaningful dots are small blue dots on some lines, and there has to be an even number of them on each line.
In practice, one card in each deck will contain the group identity, so this card is typically removed from such games. Leaving it in would allow anyone to add it to any other set they found, getting a free point (if the score is the number of cards for each set). Thus, the actual deck size contains 1 fewer card than the corresponding group.
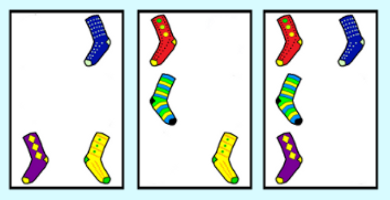
One famous example of such an extension of SET that wasn't shown in the Numberfile video is often called "ProSet" (short for Projective Set). It is usually marketed under other names, for example, "Socks". It is played on the group F26 with the identity card removed, making the deck 63 cards. The cards each contain some non-empty subset of 6 colored dots/socks. A set is any group of cards where each color appears an even number of times. This is equivalent to adding vectors in F26 and having them add to the identity: the zero vector. Since the group operation is addition, which is commutative, the sets found do not need to be in a particular order. The picture shows a set in the game of Socks.
However, there is a fundamental difference between the classic game of SET and the extensions we have talked about. No card in the SET deck obviously corresponded to the identity and had to be removed. It is almost as if the SET group "forgot" about its identity element. A group that has "forgotten" about its identity can be informally called a torsor. A torsor has a more sophisticated definition, but this casual one will do for our purposes. We also note that SET sets always contain exactly three cards. The sets have the following property: if we had chosen a particular assignment of the values of 0, 1, and 2 to each property, as in the Numberphile video, we would find that changing this assignment would have the following effect: if the initial set has all attributes different, the set will not change; if the attributes are all the same, each value would be shifted by the same shift s. The sum would thus be shifted by 3s = 0, as we look at everything mod 3.
Another affine game is a game of EvenQuads played on a deck of size 64. Each card has 3 attributes with 4 values each. Each card has symbols of a color (red, yellow, green, or blue), a shape (spiral, polyhedron, circle, square), and a quantity (from 1 to 4). The set, called quad in this game, consists of four cards such that for each feature, one of three things is true: 1) all of the cards are the same, 2) all of the cards are different, and 3) the card's values are divided fifty-fifty. The picture shows the set in this game.

Can we extend the notion of a torsor to ProSet? The answer is yes! EvenQuads is almost equivalent to the game of ProSet: you just need to pick the card corresponding to the origin and only allow sets with four cards. The four values of each attribute in EvenQuads represent all possible values of 2 different socks in ProSet/Socks. With 3 attributes, we can express all possible values of 6 dots/socks. This is more restrictive than the set that we could choose in ProSet, but the advantage is that our deck is now completely free of a choice of a particular identity value. ProSet can be used to play EvenQuads and vice versa (with the exception of the identity card); the "torsor-ness" of EvenQuads makes the definition of a set cleaner. Indeed, a set in EvenQuads is not any set of cards that forms a set in ProSet. See more about how different famous card games are equivalent to each other in the paper Card Games Unveiled: Exploring the Underlying Linear Algebra.
At this point, it is worth noting that nothing about the games of SET, ProSet, or EvenQuads requires the exact dimension chosen. The game of SET uses C3 as an underlying group and chooses to use 4 copies of it. Both ProSet and EvenQuads use 6 copies of C2. The choice of dimension, the number of copies, is usually made with practical considerations in mind to make the number of cards in the deck, 81 and 64, respectively, to be of a reasonable quantity. However, to design a new game, we only have to verify that the underlying group is satisfactory, and only then do we need to fix a dimension.
So, how would we generalize further? If each attribute was an element of Z4 instead of Z22, would that work? Recall that in the game of SET, we require three cards to sum to zero in Z32. In ProSet and EvenQuads, we also require the cards to sum to zero in Z26, where in ProSet, we use any number of cards, and in EvenQuads, we use four cards. Coming back to Z4, suppose we announce that x cards form a set if their sum is zero. If we want the cards that are all the same in each feature to form a set, we need x to be divisible by 4. If we choose x to be 4, we will lose the ability to select "all different" as a valid combination of attributes since 0+1+2+3 = 2 mod 4. Any other x that is divisible by 4 is too big to play. And in any case, we lose symmetry between different values. For example, when the attributes are divided fifty-fifty, sometimes they sum to zero, as in 1+1+3+3, and sometimes not, as in 1+1+2+2.
Is this it? Should we stop there? Let's not. Let's check Z5. To allow all cards to be the same, we will claim that sets must have 5 cards. The good news is that 0+1+2+3+4 = 0 mod 5. Suppose we define the set as 5 cards that sum to zero modulo 5. The big question is, can we define the rule without assigning the exact values to each attribute? Let's look at an example of a set: 0,0,0,2,3. We can't claim a set to be three of the same values, and two others are different. However, if we specify a relative order of our elements and allow 0,0,0,2,3 to be a set, then together with it, all shifted sequences correspond to a set; for example, shifting by 1 produces 1,1,1,3,4.
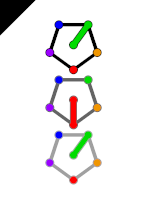
In particular, to make a game based on Z5, we can demand that our sets consist of 5 cards that add to the identity. The fact that each set has 5 cards means that we can use a torsor and do not need to explicitly specify the identity. If we represent our 5 attributes as points on a pentagon or lines pointing in one of 5 directions, we observe a remarkable pattern: the 5 values add to 0 exactly when there is a line of symmetry in the chosen attributes! Below, we see all possible ways to add 5 values mod 5 and arrive at 0, up to rotations. As an example, if we chose 3+2+1+2+2=0 mod 5, we would see that this corresponds to the second symmetry in the picture, which we can view as drawing an axis of symmetry "through the 2".

This is a property unique to the number 5, and also for numbers smaller than 4. This is not true for larger sizes of groups; for example, 0+0+0+1+2+3=6 has no symmetries in Z6. Number 4 represents an interesting case. If we represent our 4 attributes as points on a square or lines pointing in one of 4 directions, we observe that when the 4 values add to 0, there is a line of symmetry in the chosen attributes. However, in the case of values 0, 0, 3, 3, or, 0, 1, 2, 3, there is a line of symmetry, but the values do not sum to zero.
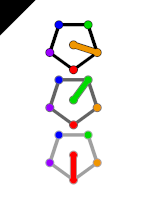
So we have shown that a torsor of C5, the cyclic group of 5 elements, might make for a convenient group on which to play a variant of SET. A reasonable choice of dimension might be 3, making a deck of size 125. This game would then be played on a C53-torsor. This inspired the name of this game as, this has been shortened to C53T, pronounced "C-Set". To illustrate a card, we use pentagons with an indicated vertex to denote an element of C5. We need 3 pentagons, one for each dimension. To help players work around the fact that cards often get turned around, each direction on each pentagon is assigned a color to help players tell them apart better. Additionally, the three pentagons are shaded to clarify which pentagon corresponds to each dimension. In the image below, we see a C53T set, where the symmetric axes in each of the three dimensions go through the red, orange, and "any" axes from top to bottom.
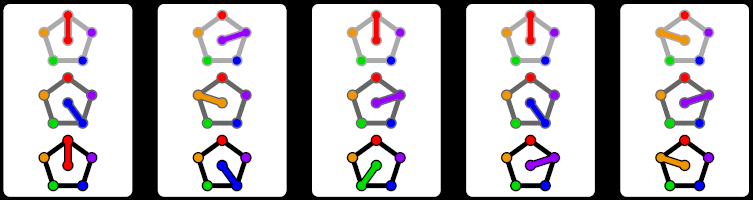
This and many other games can be found on tsetse website. The website has a description, and also allows for a solitaire play.
Finding sets in C53T is extremely hard, so this is not a game for casual players, but it does serve to illustrate what really makes a set a set. In everything discussed in this blog post, we either used a group with a clear identity (such as in the Numberphile video) or a commutative operation (such as in C53T). Is there any way to have a non-abelian group torsor to play a variant of SET? The answer is yes, but that is a story for another day.
A foam is a finite 2-dimensional CW-complex with extra properties. This one opening sentence is already more advanced than any of my usual blog posts. Let me define a finite 2-dimensional CW-complex in layman's terms.
To construct such a CW-complex, we can start with a bunch of discrete points. This will be the 0-dimensional part of our future CW-complex. To continue, we glue-in segments between some pairs of points, making the whole thing into a 1-dimensional CW-complex. We can view such a complex as a graph. Now, what we have left to do is glue some disks in. There are two ways to do it. First, we can take the disk's border and attach it to one of the points. Second, we can glue the border of the disc to a cycle in a graph.
The previous paragraph explained how to construct a finite 2-dimensional CW-complex. Foams have additional properties. Given a point in the CW-complex, its neighborhood needs to be homeomorphic to one of three objects:
Some of the coolest foams are tricolorable. A foam is called tricolorable if it is possible to color its faces each in its own color by using three colors total so that at the seams, the faces of all three colors meet.
I first heard about foams during my brother Mikhail Khovanov's lecture. He made a fascinating claim about tricolorable foams. If you remove regular points of a particular color from a foam, then the neighborhood of each point is an open disc. I was so curious, I decided to make a physical model. My readers know I hate crocheting, so I thought making a model out of felt would be easier. Thus, I made a tricolored neighborhood of a singular point. The two pictures show the same model from different angles.


Then, I needed to check my brother's statement and made the same model with one color attached to the foam by zippers. This way, I can actually unzip one color and see the result. This color in real life is neon-green but looks yellowish in the pictures.


Guess what? The result was a smooth neighborhood isomorphic to an open disc. My brother was right!
Here is another riddle I discovered in a book and gave as homework to my students.
Puzzle. I can use the number 20 thrice to make 60: 20 + 20 + 20 = 60. Make it 60 again by using a different number three times.
The book's answer was to use 5: 55 + 5 = 60.
My students were very inventive. All of them solved the puzzle, but only one out of ten students came up with the book's answer.
When I was in 8th grade, I was selected to be part of the Moscow math team and went to Yerevan, Armenia, to participate in the All-Soviet Math Olympiad. A group of us boarded a bus, and Alexander Karabegov paid for all of our bus tickets. He was from Yerevan himself and wanted to be a gracious host. I was impressed. The next time I met him was when I started studying at the Moscow State University. We have been friends ever since. He was even the best man at one of my weddings. Now, he lives in Texas and sends me his original puzzles from time to time. Today, he sent me a new one.
WARNING. His solution to the puzzle is also included. So if you want to solve it yourself, stop reading after the next paragraph.
Puzzle. A number c is called a fixed point of a function f, if it is a solution of the equation f(x) = x; that is, if f(c) = c. Find all solutions of the equation g(g(x)) = x, where g(x) = x2 + 2x − 1; that is, find all fixed points of the function f(x) = g(g(x)). (We can assume that x is a real number.)
I gave the puzzle to my students, and they converted it to a fourth-order equation, which they solved using various methods. What I liked about Alexander's solution is it only uses quadratic equations. I am too lazy to give his full solution. Here is just his solve path.
Solve path. If c is a fixed point of the function g(x), then it is a fixed point of f(x) = g(g(x)). Solving the equation g(c) = c gives us two fixed points. We need two more, as our equation is quartic. Suppose a is another fixed point. Let b = g(a). It follows that g(b) = a. Moreover, we can assume that a is not b, as we covered this case before. We get two equations a2 + 2a − 1 = b and b2 + 2b − 1 = a. Subtracting one equation from another, we get a quadratic equation that has to be divisible by a −b. As b is not a, by our assumption, we can divide the result by a − b, expressing b as a linear function of a. We plug this back into one of the two equations and get a quadratic equation for a, supplying us with the remaining two solutions. TADA!
Here's one by Sergei Luchinin, designed for 7th graders.
Puzzle. We have an 8-by-8 chessboard, but it's not colored in the usual checkerboard pattern. Instead, all cells in odd-numbered columns are black, and all cells in even-numbered columns are white. A limping rook is placed in the lower-left corner and can only move one cell to the right or one cell up. The rook's goal is to reach the upper-right corner.
The question is: Are there more paths that pass through more white cells, or more that pass through more black cells?
Here is a new report of interesting homework solutions from my students.
Puzzle. One day, two sisters decided to clean the old shed at the bottom of their garden. When they finished cleaning, one had a dirty face and the other had a clean face. The sister with the clean face went and washed her face, but the girl with the dirty face did not wash. Why should this be so?
The expected answer: The sister with the clean face saw her sister's dirty face and assumed her own face must be dirty as well, so she washed it. The sister with the dirty face saw her sister's clean face and assumed her own face must also be clean, so she didn't feel the need to wash.
Another student suggested a different but quite realistic answer.
The realistic answer: The sisters' home ran out of water after the clean sister washed her face, preventing the dirty sister from washing her own.
The other student watched too many sitcoms.
The sitcom answer: The sister with the dirty face purposefully kept her face dirty, so she could show her parents that she did all the work, as she was the only one with dirt on her face.
I asked ChatGPT to solve the puzzle, and, unsurprisingly, it came up with the standard answer. I pushed and got the following.
The ChatGPT answer: The sister with the clean face washed up because she was an Instagram influencer and couldn't risk being seen dirty, even in her own garden. Meanwhile, the sister with the dirty face was a carefree adventurer who believed dirt was "nature's makeup." Plus, she figured that if she waited long enough, the dirt would either blow away or blend into a trendy new skincare routine—"Exfoliation by Shed Dust."
Here's a fresh challenge from the recent Tournament of the Towns, crafted by Alexander Shapovalov.
Puzzle. A mother and her son are playing a game involving cheese and butter. The son starts by cutting a 300-gram block of cheese into 4 pieces. Then, the mother divides 280 grams of butter between two plates. Afterward, the son places the cheese pieces onto these same plates. The son wins if, on both plates, there is at least as much cheese as butter. If not, the mother wins. Can either the mother or the son guarantee a win, regardless of the other's moves?
A while ago I took writing lessons with Sue Katz. Below is my homework from 2010 (lightly edited). If I remember correctly, this piece was inspired by Sam Steingold.
—My friend Sam installed six locks on his door to protect himself from burglars.
—I know. I visited your friend. He has six very cheap locks. Any professional could open one in a second, so Sam's door will only resist for six seconds.
—Yeah, but those locks aren't completely identical. Three of them unlock with a clockwise motion, and three with a counterclockwise motion.
—So what? The thieves will just turn the lock mechanism whichever way it can be turned.
—Not so fast. Sam never locks all of them. Every time, he randomly picks which ones to lock.
—That might work, but what if he forgets which ones he locked?
—That's okay, He remembers which way to turn every lock to unlock.
I love hat puzzles, and this one, posted on Facebook by Konstantin Knop, is no exception.
Puzzle. The sultan decided to test his three sages once again. This time, he showed them five hats: three red and two green. Each sage was blindfolded and had one hat placed on their head. When the sages removed their blindfolds, they could see the hats on the other sages but not their own. The twist in this puzzle is that one of the sages is color-blind and cannot distinguish red from green. The sages are all friends and are aware of each other's perception of color. The sages are then asked, in order, if they know the color of their hats. Here's how the conversation unfolded:The question is: Who is color-blind?
- Alice: I do not know the color of my hat.
- Bob: Me too, I do not know the color of my hat.
- Carol: Me too, I do not know the color of my hat.
- Alice: I still do not know the color of my hat.
From time to time, the homework for my PRIMES STEP students includes questions that are not exactly mathematical. Last week, we had the following physics puzzle.
Puzzle. A fisherman needed to move a heavy iron thingy from one river's shore to another. When he put the thingy in his boat, the boat lowered so much that it wasn't safe to operate. What should he do?
The expected answer: He should attach the thingy to the bottom of the boat. When the object is inside the boat, the boat needs to displace enough water to account for the entire weight of the boat and the thingy. When the thingy is attached to the bottom of the boat, the thingy experiences its own buoyancy. Thus, the water level rises less because the thingy displaces some water directly, reducing the boat's need to displace extra water. Thus, the amount of weight the fisherman saves is equal to the amount of water that would fit into the shape of this thingy.
As usual, my students were more inventive. Here are some of their answers.
Also, some funny answers.
And my favorite answer reminded me of a movie I recently re-watched.



Before moving to the US, I attended the Gelfand seminar and took some pictures. I was a regular participant and have some bittersweet memories from that time. I've written about my experiences in several blog posts related to Gelfand, who was my advisor.
The year was 1990, and I just acquired my first camera. I was about to leave the USSR for the US and took a bunch of pictures of family, friends, and other moments. I wasn't happy with the photos I captured at the seminar due to the poor quality of the camera and the dim lighting in the lecture hall. For context, the seminar was held on Mondays from 7 to 10 pm. So I put the pictures away and forgot about them.
Recently, I decided to digitize all of my old pictures. While the seminar photos are still grainy, they feel more precious now. Perhaps it's the fact that they've survived for over 30 years, or maybe I've just grown more sentimental.
A big part of the seminar was the networking that happened beforehand. Although the seminar was scheduled to start at 7 pm, it often began at random times, anywhere between 7 and 8:30 pm. Gelfand disliked tardiness, so everyone would arrive by 7 and hang. All of my photos were taken before the seminar: some in the hallway and some in the seminar room.



In the last three pictures, the socializing had ended, and the seminar was about to start.



The term fibonometry was coined by John Conway and Alex Ryba in their paper titled, you guessed it, "Fibonometry". The term describes a freaky parallel between trigonometric formulas and formulas with Fibonacci (Fn) and Lucas (Ln) numbers. For example, the formula sin(2a) = 2sin(a)cos(a) is very similar to the formula F2n = FnLn. The rule is simple: replace angles with indices, replace sin with F (Fibonacci) and cosine with L (Lucas), and adjust coefficients according to some other rule, which is not too complicated, but I am too lazy to reproduce it. For example, the Pythegorian identity sin2a + cos2a = 1 corresponds to the famous identity Ln2 - 5Fn2 = 4(-1)n.
My last year's PRIMES STEP senior group, students in grades 7 to 9, decided to generalize fibonometry to general Lucas sequences for their research. When the paper was almost ready, we discovered that this generalization is known. Our paper was well-written, and we decided to rearrange it as an expository paper, Fibonometry and Beyond. We posted it at the arXiv and submitted it to a journal. I hope the journal likes it too.
Consider the following Fibonacci trick. Ask your friends to choose any two integers, a and b, and then, starting with a and b, ask them to write down 10 terms of a Fibonacci-like sequence by summing up the previous two terms. To start, the next (third) term will be a+b, followed by a+2b. Before your friends even finish, shout out the sum of the ten terms, impressing them with your lightning-fast addition skills. The secret is that the seventh term is 5a+8b, and the sum of the ten terms is 55a+88b. Thus, to calculate the sum, you just need to multiply the 7th term of their sequence by 11.
If you remember, I run a program for students in grades 7 through 9 called PRIMES STEP, where we do research in mathematics. Last year, my STEP senior group decided to generalize the Fibonacci trick for their research and were able to extend it. If n=4k+2, then the sum of the first n terms of any Fibonacci-like sequence is divisible by the term number 2k+3, and the result of this division is the Lucas number with index 2k+1. For example, the sum of the first 10 terms is the 7th term times 11. Wait, this is the original trick. Okay, something else: the sum of the first 6 terms is the 5th term times 4. For a more difficult example, the sum of the first 14 terms of a Fibonacci-like sequence is the 9th term times 29.
My students decided to look at the sum of the first n Fibonacci numbers and find the largest Fibonacci number that divides the sum. We know that the sum of the first n Fibonacci numbers is Fn+2 - 1. Finding a Fibonacci number that divides the sum is easy. There are tons of cute formulas to help. For example, we have a famous inequality F4k+3 - 1 = F2k+2L2k+1. Thus, the sum of the first 4k+1 Fibonacci numbers is divisible by F2k+2. The difficult part was to prove that this was the largest Fibonacci number that divides the sum. My students found the largest Fibonacci number that divides the sum of the first n Fibonacci numbers for any n. Then, they showed that the divisibility can be extended to any Fibonacci-like sequence if and only if n = 3 or n has remainder 2 when divided by 4. The case of n=3 is trivial; the rest corresponds to the abovementioned trick.
They also studied other Lucas sequences. For example, they showed that a common trick for all Jacobsthal-like sequences does not exist. However, there is a trick for Pell-like sequences: the sum of the first 4k terms (starting from index 1) of such a sequence is the (2k + 1)st term times 2P2k, where Pn denotes an nth Pell number.
You can check out all the tricks in our paper Fibonacci Partial Sums Tricks posted at the arXiv.
Have you heard of Grigori Perelman? If you like math, you probably have. He is one of the most renowned mathematicians in the world. I recently got a book on the Leningrad Mathematical Olympiads (scheduled for publication in English in 2025) and found Grigori's name there. He authored one of the Olympiad problems from 1984. For context, he was born in 1966. Here it is.
Puzzle. You are given ten numbers: one "1" and nine "0"s. You are allowed to replace any two numbers with their arithmetic mean. What is the smallest number that can appear in place of the "1" after a series of such operations?
The famous 5-card trick begins with the audience choosing 5 cards from a standard deck. The magician's assistant then hides one of the chosen cards and arranges the remaining four cards in a row, face up. Upon entering the room, the magician can deduce the hidden card by inspecting the arrangement. To eliminate the possibility of any secret signals between the assistant and the magician, the magician doesn't even have to enter the room — an audience member read out the row of cards.
The trick was introduced by Fitch Cheney in 1950. Here is the strategy. With five cards, you are guaranteed to have at least two of the same suit. Suppose this suit is spades. The assistant then hides one of the spades and starts the row with the other one, thus signaling that the suit of the hidden card is spades. Now, the assistant needs to signal the value of the card. The assistant has three other cards than can be arranged in 6 different ways. So, the magician and the assistant can agree on how to signal any number from 1 to 6. This is not enough to signal any random card.
But wait! There is another beautiful idea in this strategy — the assistant can choose which spade to hide. Suppose the two spades have values X and Y. We can assume that these are distinct numbers from 1 to 13. Suppose, for example, Y = X+5. In that case, the assistant hides card Y and signals the number 5, meaning that the magician needs to add 5 to the value of the leftmost card X. To ensure that this method always works, we assume that the cards' values wrap around. For example, king (number 13) plus 1 is ace. You can check that given any two spades, we can always find one that is at most 6 away from the other. Say, the assistant gets a queen of spades and a 3 of spades. The 3 of spades is 4 away from the queen (king, ace, two, three). So the assistant would hide the 3 and use the remaining three cards to signal the number 4.
I skipped some details about how permutations of three cards correspond to numbers. But it doesn't matter — the assistant and the magician just need to agree on some correspondence. Magically, the standard deck of cards is the largest deck with which one can perform this trick with the above strategy.
Later, a more advanced strategy for the same trick was introduced by Michael Kleber in his paper The Best Card Trick. The new strategy allows the magician and the assistant to perform this trick with a much larger deck, namely a deck of 124 cards. But this particular essay is not about the best strategy, it is about the Cheney strategy. So I won't discuss the advanced strategy, but I will redirect you to my essay The 5-Card Trick and Information, jointly with Alexey Radul.

63 years later, the 4-card trick appeared in Colm Mulcahy's book Mathematical Card Magic: Fifty-Two New Effects. Here the audience chooses not 5 but 4 cards from the standard deck and gives them to the magician's assistant. The assistant hides one of them and arranges the rest in a row. Unlike in the 5-card trick, in the 4-card trick, the assistant is allowed to put some cards face down. As before, the magician uses the description of how the cards are placed in a row to guess the hidden card.
The strategy for this trick is similar to Cheney's strategy. First, we assign one particular card that the magician would guess if all the cards are face down. We now can assume that the deck consists of 51 cards and at least one of the cards in the row is face up. We can imagine that our 51-card deck consists of three suits with 17 cards in each suit. Then, the assistant is guaranteed to receive at least two cards of the same imaginary suit. Similar to Cheney's strategy, the leftmost face-up card will signal the imaginary suit, and the rest of the cards will signal a number. I will leave it to the reader to check that signaling a number from 1 to 8 is possible. Similar to Cheney's strategy, the assistant has an extra choice: which card of the two cards of the same imaginary suit to hide. As before, the assistant chooses to hide the card so that the value of the hidden card is not more than the value of the leftmost face-up card plus 8. It follows that the maximum number of cards the imaginary suit can have is 17. Magically, the largest possible deck size for performing this trick is 52, the standard deck of cards.
Last academic year, my PRIMES STEP junior group decided to dive deeper into these tricks. We invented many new tricks and calculated their maximum deck sizes. Our cutest trick is a 3-card trick. It is similar to both the 5-card trick and the 4-card trick. In our trick, the audience chooses not 5, not 4, but 3 cards from the standard deck and gives them to the magician's assistant. The assistant hides one of them and arranges the other two in a row. The assistant is allowed to put some cards face down, as in the 4-card trick, and, on top of that, is also allowed to rotate the cards in two ways: by putting each card vertically or horizontally.
We calculated the maximum deck size for the 3-card trick, which is not 52, as for the 5- and 4-card trick, but rather 54. Still, this means the 3-card trick can be performed with the standard deck. The details of this trick and other tricks, as well as some theory, can be found in our paper Card Tricks and Information.
The famous 5-card trick begins with the audience choosing 5 cards from a standard deck. The magician's assistant then hides one of these cards and arranges the remaining four cards in a row, face up. On entering the room, the magician can deduce the hidden card by inspecting the arrangement. To eliminate the possibility of secret signals between the assistant and the magician, the magician needn't even enter the room — an audience member can call them and read out the row of cards.
We will not delve into the mechanics of the trick, which are widely available online. Instead, we will explore the information theory underlying it. Michael Kleber's paper, The Best Card Trick, provides an information-theoretic argument that works as follows:
For a deck of N cards, the number of different messages the magician can receive is N(N-1)(N-2)(N-3). The magician must guess the hidden card, which is equivalent to determining the set of five cards chosen by the audience. The number of such sets is N choose 5. For the trick to work, the number of messages must not exceed the number of possible answers, leading to the inequality: (N choose 5) ≤ N(N-1)(N-2)(N-3). After some manipulation, we get that (N-4)/120 doesn't exceed 1. This implies that the deck can have at most 124 cards. The bound turns out to be tight: as discussed in Kleber's paper, the trick can still be performed with such a huge deck. The paper expands this argument to a trick with K instead of 5 cards and shows that the maximum deck size for such a trick is K! + K - 1.
Here, we want to present a more direct, intuitive argument. We will make the argument for the 5-card trick, which is easily generalizable to the K-card trick. The assistant has 5 ways to choose which card to hide and 24 ways to arrange the remaining four cards, so they only have 120 actions in any given situation. Ergo, the magician should only be able to extract 120 alternatives' worth of information from knowing what action the assistant would take.
This is a bit fishy, because of course even with N > 120, the trick could happen to work sometimes. That is, if the magician tells the assistant the strategy by which they will guess the missing card, the assistant may, for some sets of 5 cards drawn even from a large deck, manage to show an arrangement of four that will lead the magician to guess correctly.
The crux of formalizing the argument is to move to the global view, but we can do that without additional computations. Consider the space of all states reachable by any strategy of the assistant. In our case, this is equivalent to ordered sequences of five cards, with the last face down. There are obviously (N-4)M of these, where M is the number of states the magician observes (four-card sequences, in our case), however many of those there are. When the assistant and the magician choose a strategy for the assistant, they make most of these impossible. Indeed, since the assistant always has exactly 120 options, after they have chosen one to take in each situation, we have exactly (N-4)M/120 states that remain possible with that strategy. For the trick to always work, this last expression must be no more than M; M cancels, saving us the trouble of computing it, and we are left with N-4 ≤ 120 as desired.
By the way, one of the authors of this essay, Tanya Khovanova, taught this trick to her PRIMES STEP students, who were students in grades 7 through 9. They found and studied interesting generalizations of this trick and wrote the paper Card Tricks and Information available at the arXiv. They studied many variations of the trick, including the ones where the assistant is allowed to put the cards face down. This interesting variation is outside the scope of this essay.
We would like to use as an example one of the tricks described in the paper: the K-card trick, where the assistant hides one card and arranges the rest in a circle. The implication is that when the audience member describes the arrangement to the magician, they describe the circle clockwise in any order. Our argument works here as follows. We count the number of the assistant's actions: K ways to choose the hidden card and (K-2)! ways to arrange the cards in different circles up to rotation. Thus, the number of different actions is K(K-2)!. Hence, the deck size doesn't exceed K(K-2)! + K - 1, as we can exclude the K-1 cards in the circle, as they aren't hidden. Not surprisingly, this is the same formula as in the paper.
The puzzle In the Details by Derek Kisman is one of my favorite MIT Mystery Hunt puzzles of all times. I even wrote a blog post advertising it and another post with comments on the solution. This puzzle type became known as fractal word search.
In the standard word search, you have a grid of letters and a list of words. You need to find the words written in the grid in all eight directions. The unused letters provide the answer, or a clue to the answer, of the word search puzzle.
In the fractal word search, you have a grid of letters and a list of words. It looks like a regular word search, but you will not find all the words inside the given grid. The given grid is only a snapshot of the whole grid on some particular level k. To go to level k+1, you have to use replacement rules: each letter is replaced by a 2-by-2 block of letters. This creates a much bigger grid where you might find more words from the given list.
An interesting question is, where do you find the replacement rules? In Derek's puzzle, the rules were not given, but the initial grid was level 2. So you could notice that this grid can be decomposed into 2-by-2 squares, and there are only 26 different squares, implying that each square corresponds to a letter. Assuming that replacing the 2-by-2 squares with correct letters will allow you to find more words from the list, you can decipher the replacement rules. This will allow you to get to level 1 as well as any other level. Small levels are easy to search, but on large levels, the grid gets so huge that it might not fit in the memory of a computer, or a million computers. That is why this puzzle was presented at the MIT mystery hunt, but not at any other puzzle hunt. It is quite difficult: one of the given words is hiding on level 86.
I liked the puzzle so much, I included it in one of my lectures. After I gave my talk at Brown University, a student, Klára Churá, approached me. She got as fascinated with the puzzle as I was. We ended up collaborating on the paper Fractal Word Search: How Deep to Delve. As the title suggests, we focused on finding the upper bound of the level where we could find a word of a given length. We had two parameters: the size of the alphabet n and the block size b used in the replacement rules.
For different reasons, the most interesting case is words of length 3. I will leave it to the reader to figure out why this is the most interesting case, or the reader can check our paper. We showed that any word of length 3 appears no later than level n3 + n2 + 1.
When we posted the paper, I sent the link to Derek. He immediately wrote a program and showed that our bound is fairly tight. His code is available at GitHub. He created a configuration that puts a 3-letter word at depth LCM(a,b,c)+1, where a,b,c ≤ n-3. If n is even, this gives us a lower bound of (n-3)(n-4)(n-5) + 1. If n is odd, this gives us a lower bound of (n-4)(n-5)(n-6) + 1. In any case, asymptotically, it is very close to our upper bound.
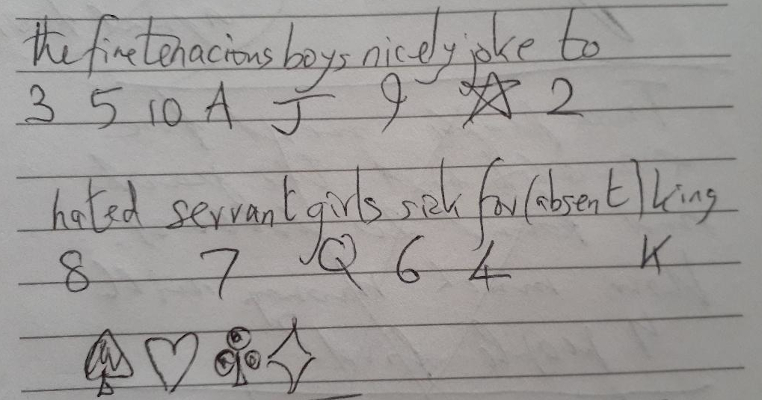
The fine tenacious boys nicely joke to hated servant girls sick for (absent) king.
The picture shows John Conway's notes in my journal. They are the mnemonic for setting up his trick. For example, the word "tenacious" sounds similar to "ten" and "ace". Hence, we arrange 13 cards in this order: 3, 5, 10, A, J, 9, joker, 2, 8, 7, Q, 6, and 4. We also put the king aside. The trick looks better if the cards are the same suit.
The fun part of the trick is the story he told while showing it. Unfortunately, I do not remember the story. My only other note says:
One, two, three are done by me. Four, five, six: they do the tricks. Seven, eight, play them straight. We all try nine for quite a long time. The king is back.
Here is my attempt to recover the trick. We arrange the cards in the above order. We keep the cards face down so that the three is on top. Now, we spell the word "ACE", and for each letter, we move one card from the top to the bottom of the pile. Then, we flip the next card from the top of the pile, and "tada", the card is an ace. We put it aside. Now, we repeat the process by spelling "TWO", and the next card after that is a two. We do the same for "THREE".
But, when we try the same process for "FOUR", we get the joker instead. This is not surprising if you remember that "Four, five, six: they do the tricks". We put the joker at the bottom of the pile and continue. In the next round, after spelling "FOUR" again, we get 4, which we put aside. We proceed by spelling "FIVE" and getting a joker, then getting 5 after the second spelling. The same happens with "SIX". Then we continue with "SEVEN" and "EIGHT" without getting the joker.
Then, we try "NINE", and get the joker. Then, we spell it again and again and keep getting the joker. Clearly, we are in a cycle that can go on forever. If you recall the quote, "We all try nine for quite a long time." To get out of this cycle, we remember our king and put it on top of the pile when the joker is on the bottom. We start again. And now we can spell "NINE" and get 9. We are back to normal with "TEN", "JACK", and "QUEEN", too. The king, however, appears on the second try after spelling "KING", getting the joker, and spelling "KING" again.
I do not remember the details of John's performance. I tried to find the trick online but only saw it briefly mentioned in Mathematics, Magic, and Mischief with John H. Conway.
Have you seen this trick? Any juicy details are welcome in the comments.

Recent Facebook Puzzle from Denis Afrisonov.
Puzzle. 100 students took a test where each was asked the same question: "How many out of 100 students will get a 'pass' grade after the test?" Each student must reply with an integer. Immediately after each answer, the teacher announced whether the current student passed or failed based on their answer. After the test, an inspector checks if any student provided a correct answer but was marked as failed. If so, the teacher is dismissed, and all students receive a passing grade. Otherwise, the grades remain unchanged. Can the students devise a strategy beforehand to ensure all of them pass?
(A small piece I wrote on Dec 29, 2009. Edited in 2024.)
They were black, very comfy, and felt like a second skin. The shoes had this shock-absorbing cushioning, so asphalt felt like carpet.
I had them for 10 years. They served me for so long that I started believing our happy relationship would last forever.
First, I noticed that they are not black anymore. They acquired a greenish color. Then, the sound changed. Steps started sounding like farts. I trusted my shoes so much that, at first, I thought I was just getting old. But I realized that I couldn't be that perfect: I couldn't possibly fart with such a precise rhythm. Besides, I should have run out of gas from time to time.
When I came home, I took off my shoes and looked at them. The sole of one shoe was gone. My love affair with my shoes was over. Oh well. The divorce was easy. They went to my garbage can. No tears, no broken hearts, just a lost sole.
I recently posted a symmetry puzzle from Donald Bell. He just sent me another one.
Puzzle. Start with a 30-60-90 triangle (half of an equilateral triangle). Divide it into two 30-60-90 triangles of different sizes by dropping a perpendicular from the right-angled corner to the opposite side. Put the resulting two pieces together to form a symmetrical shape. There are two solutions.
It took me some time to find the second solution. I love this puzzle.
Usually, I only post puzzles to which I know the solution. However, I don't know the solution to this exciting geometry question from Facebook, yet. But I like the puzzle so much that I'd rather post it than wait until I find time to think about it.
Puzzle. A centrally-symmetric figure is cut into two equal polygons: A and B. Is it possible that the center of symmetry is in A but not in B?
I run a program at MIT called PRIMES STEP, where we conduct mathematical research with children in grades 6 through 9. Our first research project was about a funny coin called an alternator. This coin exists only in a mathematician's mind as it can change weight according to its own will. When you put the alternator on the scale, it can either weigh the same as a real coin or a fake coin (the fake coins are lighter than real ones). The coin strictly alternates how much it weighs each time it is put on the scale. My colleague, Konstantin Knop, recently sent me a fresh alternator puzzle.
Puzzle. There are four identical-looking coins: two real, one fake, and one alternator. How do you find the alternator using a balance scale at most three times?
I am not as excited about the MIT Mystery Hunt as I used to be. So, for this year's hunt, I didn't go through all the puzzles but present here only the puzzles that were recommended to me. I start with math, logic, and CS.
Then we have some word puzzles.
Now, the rest.
Here is an old joke.
A former student runs into an old calculus teacher as she is shuffling home. The student is happy to see her and says, "I recently thought about you and our classes." "How so?" she perks up. "I was in a bit of a pickle when calculus helped me," he says. The old lady straightens, and her face begins to glow. "Can you elaborate?", asks the teacher in anticipation. The student proceeds with his story. "I was walking home in the pouring rain when a gust of wind snatched my hat right off my head. The hat landed in a puddle. This wasn't just any hat; it was a gift from my dad, so I really wanted to get it back. But I didn't exactly fancy diving headfirst into the puddle. So, I looked around and saw a piece of wire. I bent it into the shape of an integral and used it to fetch my hat."
Foams are a recent craze in homology theory. I want to explain what a foam is using a tesseract as an example. Specifically, the 2D skeleton of a tesseract is a foam.
We can view a tesseract as a convex hull of 16 points in 4D space with coordinates that are either 0 or 1. The edges connect two vertices with the same three out of four coordinates. Faces are squares with corners being four vertices that all share two out of four coordinates.
Foam definition. A foam is a finite 2-dimensional CW-complex. Each point's neighborhood must be homeomorphic to one of the three objects below.
My favorite example of a foam is a tesseract. Or, more precisely, the set of tesseract's vertices, edges, and faces form a foam.
Some of the coolest foams are tricolorable. A foam is called tricolorable if we can color it using three colors in such a way that each face has its own color, and any three faces that meet at a seam are three distinct colors.
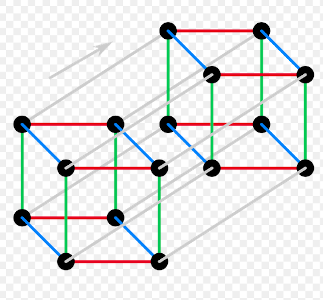
Not surprisingly, I chose a tricolorable foam for our example. Let me prove that the tesseract's 2D skeleton is tricolorable. We start by coloring the edges in four colors depending on the direction: red, green, blue, or gray, as in the first picture (source: Wikipedia). Each face has two pairs of edges of two different colors. We can color the faces in the following manner: if none of the edges are gray, then the face color is the complementary non-gray color (For example, if the edges are red and blue, the face is green). If the edges are gray and one other color, then the face color matches the non-gray color (For example, if the edges are red and gray, the face is red). I leave it to the reader to prove that this coloring means that each edge is the meeting point of three different face colors.
Here is an interesting property of tricolorable foams. It is Proposition 2.2 in the paper Foam Evaluation and Kronheimer-Mrowka Theories, by Mikhail Khovanov and Louis-Hardien Robert.
Proposition. If we remove the regular points of one particular color from a tricolored foam, we will get a closed compact surface containing all the seam points and singular vertices.

In our example, the result is a torus, which you can recognize in the second picture. Here, I use the Schlegel diagram as a model for a tesseract, shown on the right (source: Wikipedia). The exercise for the reader is to explain where the eight green faces of the torus were before they were removed.
The following lemma from the aforementioned paper describes another cool property of a tricolorable foam.
Lemma. If a foam is tricolorable, its 1D skeleton (the graph formed by seams and singular points) is bipartite.
And, surely, I am leaving it up to the reader to check that the tesseract's 1D skeleton forms a bipartite graph.
Here is a cool puzzle I heard from Tiago Hirth at the last Gathering for Gardner, who in turn heard it from Donald Bell.
Puzzle. You have three L-tetrominoes. Arrange them on a plane without overlaps so that the resulting shape has a line of symmetry.


Here is an old joke.
A cat is chasing a mouse, and the mouse hides into its little hole. While it's in there, the mouse hears some barking, "Woof! Woof!" Smart mouse figures a dog scared off the cat, so it peeks out. But guess what? Cat's still there and catches the mouse, saying, "See, that's why it pays to know foreign languages!!"
I recently bought a book by Evdokimov, titled Hundred Colors of Math. The book has lovely math puzzles and cute pictures. The book has answers but doesn't explain them. Also, the English translation is decent but not perfect. For these two reasons, I am not sure I would recommend the book. However, I do like the puzzles, and here is one of them, called Runaway Cell.
Puzzle. The figure depicted in the picture (a 6-by-6 square, in which the top row is moved by one square) was cut along the grid lines into several identical parts which could be put together to form a 6-by-6 square. The parts are allowed to be turned over. What is the minimal possible number of such parts?

I gave a short talk about my favorite math jokes at G4G15. G4G stands for the Gathering for Gardner, my favorite conference. Here is a joke about Heisenberg from my talk.
* * *
Heisenberg gets pulled over on the highway.
Cop: "Do you know how fast you were going, sir?"
Heisenberg: "No, but I know exactly where I am."
After my talk, David Albert sent me a sequel to this joke.
* * *
Heisenberg gets pulled over on the highway.
Cop: "Do you know how fast you were going, sir?"
Heisenberg: "No, but I know exactly where I am."
Cop: "You were going 85 miles per hour".
Heisenberg: "Oh great—now I'm lost!"
Here is another joke from the conference.
* * *
—Did you hear about the mathematician who's afraid of negative numbers?
—He'll stop at nothing to avoid them.
This joke, too, got an awesome sequel from Jesse Lauzon.
* * *
Did you hear about the mathematician who is afraid of negative numbers?
—He'll stop at nothing to avoid them.
—Well, that's only natural!
Here is the most recent addition to my collection from my friend, Alexander Karabegov.
* * *
A trigonometry professor lost his voice and had to use sine language.
Another cute geometry puzzle was posted on Facebook.
Puzzle. An equilateral triangle in a plane has three vertices with known x-coordinates: a, b, and c. What is the side of the triangle?
I want to describe three different solutions that the readers of the Facebook channel posted. But before doing so, let's look at the problem's symmetries. We can immediately say that the answer should be a symmetric function of three variables: |a-b|, |b-c|, and |c-a|. It is possible to coordinate-bash the problem. However, I always prefer geometric solutions. Having said that, if one wants a calculation, using complex numbers might speed things up.
A solution using complex numbers. Suppose c is the origin, then the first vertex corresponds to a complex number a+xi. Then, the second vertex can be found after rotating the first vertex around the origin by 60 degrees. That means it is at (a+xi)exp(±2πi/6). Without loss of generality, we can assume that the second vertex corresponds to (a+xi)(1+i√3)/2. It follows that b = (a−x√3)/2. Thus, x = 2(a/2-b)/√3. And the side length is √(a2+x2) = √(4(a2-ab+b2)/3). Adjusting for the choice of the origin, we get that the length is √(2((a-b)2+(b-c)2+(c-a)2)/3).
A geometric solution. Draw a line through point A parallel to the x-axis. Denote the intersections of this line with lines x=b and x=c as P and Q, correspondingly. Let R be the midpoint of the side BC. Then, the triangle PQR is equilateral. To prove it, notice that angles ARC and AQC are right, which implies that points ARCB are on the same circle with diameter AC. It follows that the angles RCA and RQA are the same; thus, the angle RQA is 60 degrees. Given that the triangle PQR is isosceles as R has to be on the bisector of PQ, we conclude that the triangle PQR is equilateral. Now, we can calculate the height of PQR and, therefore, the height of ABC, from which the result follows.
A physics solution. Without loss of generality, we can assume that a+b+c=0. Thus, the y-axis passes through the triangle's centroid. The moment of inertia of the system consisting of the three triangle vertices with respect to the y-axis is a2 + b2 + c2. Now, we add the symmetry consideration: the inertia ellipse must be invariant under the 60-degree rotation, implying that the ellipse is actually a circle. This means that the inertia moment doesn't change under any system rotation. Thus, we can assume that one of the vertices lies on the y-axis. In this case, the inertia moment equals L2/2, where L is the length of the triangle's side. The answer follows.
The homework I give to my students (who are in 6th through 9th grades) often starts with a math joke related to the topic. Once, I decided to let them be the comedians. One of the homework questions was to invent a math joke. Here are some of their creations. Two of my students decided to restrict themselves to the topic we studied that week: sorting algorithms. The algorithm jokes are at the end.
* * *
A binary integer asked if I could help to double its value for a special occasion. I thought it might want a lot of space, but it only needed a bit.
* * *
Everyone envies the circle. It is well-rounded and highly educated: after all, it has 360 degrees.
* * *
Why did Bob start dating a triangle? It was acute one.
* * *
Why is Bob scared of the square root of 2? Because he has irrational fears.
* * *
Are you my multiplicative inverse? Because together, we are one.
* * *
How do you know the number line is the most popular?
It has everyone's number.
* * *
A study from MIT found that the top 100 richest people on Earth all own private jets and yachts. Therefore, if you want to be one of the richest people on Earth, you should first buy a private jet and yacht.
* * *
Why did the geometry student not use a graphing calculator? Because the cos was too high.
* * *
Which sorting algorithm rises above others when done underwater? Bubble sort!
* * *
Which sorting algorithm is the most relaxing? The bubble bath sort.
Here is an interesting puzzle by Ivan Mitrofanov.
Puzzle. In front of my dog, Fudge, lies an infinite number of meatballs with a fly sitting on each of them. At each move, Fudge makes two consecutive operations described below.Fudge wants to eat no more than a million flies. Assuming that flies sit still, prove that Fudge doesn't have a strategy where each meatball is eaten at some point.
- Eats a meatball and all the flies sitting on it at that time.
- Transfers one fly from one meatball to another (there can be as many flies as you want on a meatball).
I collect math jokes and, of course, show them to my family. From time to time, my family contributes. The first joke is by my son, Alexey.
* * *
When you board a train traveling East from Chicago to Boston at 60 miles an hour, you realize you are a part of the problem.
And this one is one of mine.
* * *
A dyslexic's excuse: my god ate my homework.
My grandson, Alex, heard the following famous joke.
* * *
A logician rides an elevator. The door opens, and someone asks:
—"Are you going up or down?"
—"Yes."
He created his own version.
* * *
A logician rides an elevator. The door opens, and someone asks:
—"Are you going up or down?"
"No," replies the logician and walks out.
Alex, though he is 10, is very good with words. I liked the wordplay in one of his comments.
* * *
This puzzle is confusling.
These two puzzles were given to me by Andrey Khesin.
Puzzle. My friend and I are going to play the following game at a casino. Each round, each of us (my friend, the dealer, and I) secretly chooses a black or white stone and drops it in the same bag. Then, the contents of the bag are revealed. If all three stones are the same color, my friend and I win the round. If not, we lose to the dealer. One extra caveat. I have a superpower: as soon as we sit down, I can read the dealer's mind and learn the dealer's choices for all future rounds. Unfortunately, at that time, it's too late for me to give this information to my friend and win all the rounds. The only thing we can do is agree on a strategy before the game.
- Design a strategy to win 6 out of 10 rounds.
- Design a strategy to win 7 out of 11 rounds.
- Is it possible to win 6 out of 9 rounds?
Puzzle. In a crowd of 70 people, one person is a murderer, and another person is a witness to said murder. A detective can invite a group into his office and ask if anyone knows anything. The detective knows that everyone except the witness would say nothing. The witness is a responsible person who is more afraid of the murderer than they desire to fulfill their civic duty. If the witness is in the same group as the murderer, the witness will be silent; otherwise, the witness will point to the murderer. The detective knows this will happen and wants to find the murderer in as few office gatherings as possible. What is the minimum number of times he needs to use his office, and how exactly should the detective proceed?
* * *
—Why was the fraction worried about marrying the decimal?
—Because he would have to convert.
* * *
—How does a professional mathematician plow a field?
—With a protractor.
* * *
—How many bakers does it take to bake a pi?
—3.14.
* * *
—What did the witch doctor say after lifting the curse?
—Hexagon.
* * *
—What do you call a teapot of boiling water on top of a mountain?
—A high-pot-in-use.
* * *
—What do you call a K1 graph drawn at freezing temperature?
—An ice-olated vertex!
* * *
—What is the best way to pass a geometry test?
—Know all the angles.
* * *
—Did you hear about the over-educated circle?
—It has 360 degrees!
* * *
—What do parallel lines and vegetarians have in common?
—They never meat.
* * *
—Did you hear about the mathematician who's afraid of negative numbers?
—He'll stop at nothing to avoid them.
* * *
—What do you call a gentleman who spent all the summer at the beach?
—A tangent.
* * *
—What do mathematicians and the Air Force have in common?
—They both use pi-lots.
* * *
—Why can't a nose be 12 inches long?
—Because then it would be a foot.
* * *
—Are monsters good at math?
—Not unless you Count Dracula.
* * *
—Why did the math professor divide sine by tan?
—Just cos.
* * *
Two is the oddest prime.
There are a lot of puzzles where you need to guess something asking only yes-or-no questions. In this puzzle, there are not two but three possible answers.
Puzzle. Mike thought of one of three numbers: 1, 2, or 3. He is allowed to answer "Yes", "No", or "I don't know". Can Pete guess the number in one question?
Yes, he can. This problem was in one of my homeworks, and my students had a lot of ideas. Here is the first list were ideas are similar to each other.
One student was straightforward.
One student used a famous unsolved problem: It is not known whether an odd perfect number exists.
Then, I gave this to my grandchildren, and they decided to answer in a form of a puzzle. Payback time.
I rarely post physics puzzles, but this one is too good to pass on.
Puzzle. A wireframe icosahedron is assembled so that each of its edges has a resistance of 1. What is the total resistance between opposite vertices of the icosahedron?
While we are at it, another interesting question would be the following.
Puzzle. A wireframe cube is assembled so that each of its edges has a resistance of 1. What is the total resistance between opposite vertices of the cube?
And this reminds me of a question I heard when I was preparing for an IMO many years ago.
Puzzle. A wireframe infinite square grid is assembled so that each of its edges has a resistance of 1. What is the total resistance between two neighboring vertices?
Have you ever heard of ikigai? The Japanese concept which gives four simple requirements for a happy career:
I often think about it for myself and for my students. Is this good advice for finding a career path?
I like that ikigai separates the first two requirements: passion and gift. Many of my students do not see the difference, as passion and gift are highly correlated. When you love something, you practice it and become better at it. When you are good at something, it becomes easy and enjoyable.
Nonetheless, passion and gift are different. Unfortunately, I've seen students who are good at math only because their parents push them, but they do not love it. Some of them already found their passion but are afraid to tell their parents. Some haven't yet found their passion, but it is perfectly clear that math is not it. So, a gift doesn't imply passion.
What about the other way around? My programs are too selective, so I haven't seen students who are not gifted in math. I will use myself as an example. I have always passionately loved dancing, but it is obvious that my dancing career would have been a disaster. I am very happy I closed that career path in fifth grade.
Anyway, the first two ikigai requirements are not the same, and both are necessary.
The third ikigai requirement is about doing what the world needs. Impacting the world is a great motivator and makes you feel good. And yet, I see happy and successful mathematicians who only care about the beauty of what they are doing and nothing else. This requirement is important but might not be a deal breaker for everyone.
The last ikigai requirement is crucial. If you are not being paid for your efforts, it is not a career; it is a hobby. I got attracted to it because it includes an important caveat: you need to find people who want to pay you for what you can offer. I recently wrote an essay Follow Your Heart? about many young aspiring opera singers who ignored this last requirement and ended up changing careers.
Nevertheless, the whole concept of ikigai bugs me. People who find their dream job might agree to work for much less pay than they are worth. It opens them up to potential exploitation by greedy employers.
Have I reached my ikigai? Judging by my low pay, I am close.
My grandkids like playing a game while I drive. They look out the window to spot the cars they like and score points. A Jeep is 1, a convertible is 10, a Mini Cooper is 40, and a Bug is 100. If we are lucky and see a convertible Mini or Bug, we get 10 extra points for convertibility. I play with them, of course. As a result, I can recognize minis and bugs from hundreds of miles away (I am exaggerating).
Recently, a Mini annoyed me. I was driving behind one, warmly thinking about my grandchildren, when its right turn signal started flashing. The signal looked like an arrow pointing to the left. I got so confused that my grandkids flew from my mind.
When I came home, I started googling and discovered that Mini designers wanted the British symbolism on their cars. The right signal is reminiscent of the right half of the British flag.


Here is the picture from Reddit with the left turn signal on.

I am writing this essay but afraid to show my grandkids these pictures. They would be maxi-disappointed with Minis.
Here is the homework problem I gave to my PRIMES STEP students.
Puzzle. A man called his wife from the office to say that he would be home at around eight o'clock. He got in at two minutes past eight. His wife was extremely angry at this lateness. Why?
The expected answer is that she thought he would be home at 8 in the evening, while he arrived at 8 in the morning. However, my students had more ideas.
For example, one student extended the time frame.
Another student found the words "got in" ambiguous.
A student realized that the puzzle never directly stated why she got angry.
The students found alternative meanings to "called his wife from the office" and "minutes."
One of the perks of being a teacher is receiving congratulations not only from family and friends, but also from students. By the way, I do not like physical gifts — I prefer just congratulations. Luckily, MIT has a policy that doesn't allow accepting gifts of any monetary value from minors and their parents.
Thus, my students are limited to emails and greeting cards.
One of my former students, Evin Liang, got really creative. He programmed the Game of Life to generate a Christmas card for me. You can see it for yourself on YouTube at: Conway Game of Life by Evin Liang.
This is one of my favorite congratulations ever.
Puzzle. There are 100 cards with integers from 1 to 100. You have three possible scenarios: you pick 18, 19, or 20 cards at random. For each scenario, you need to estimate the probability that the sum of the cards is even. You do not need to do the exact calculation; you just need to say whether the probability is less than, equal to, or more than 1/2.
I like including warm-up puzzles with every homework.
Puzzle. Farmer Giles has four sheep. One day, he notices that they are all standing the same distance away from each other. How can this be so?
The expected answer: The configuration is impossible in 2D. So, one of the sheep is on a hill or in a pit.
Some students thought big: The sheep could be placed at different locations around the Earth, forming a really big tetrahedron. In this case, we need to explain what it means for the farmer to "notice", but this minor issue could be resolved in many ways.
Some of the students questioned the meaning of the word distance. They argued that if sheep are all touching each other, they are the same distance 0 from each other. One way this could happen is if the tails of the four sheep were entangled.
I loved coin puzzles, but after several research projects related to those shiny discs, I got tired of them. The fatigue was temporary, as confirmed by the following Facebook puzzle that reignited my interest.
Puzzle. There are 30 coins in a circle that look the same. However, 20 of them are fake, and the rest are real. Fake coins weigh the same, and real coins weigh the same but heavier than fake ones. You need to find as many fake coins as possible using a balance scale once, given that the fake coins are positioned consecutively. What is your strategy?
My PRIMES STEP program consists of two groups of ten students each: the senior group and the junior group. The senior group is usually stronger, and they were especially productive last academic year. We wrote four papers, which I described in the post EvenQuads at PRIMES STEP. The junior group wrote one paper related to the game SOS. The game was introduced in the following 1999 USAMO problem.
Problem. The game is played on a 1-by-2000 grid. Two players take turns writing an S or an O in an empty square. The first player who produces three consecutive squares that spell SOS wins. The game is a draw if all squares are filled without producing SOS. Prove that the second player has a winning strategy.
The solution is quite pretty, so I do not want to spoil it. If my readers want it, the solution for this grid, and, more generally, for any grid of size 1-by-n, is posted in many places.
My students studied generalizations of this game, and the results are posted at the arXiv: SOS. We tried different target strings and showed that:
Then, we tried a version where the winner needed to spell one of two target strings. We showed that:
We tried several more elaborate variations, but I want to keep this post short.
I recently posted A Quadrilateral in a Rectangle puzzle.
Puzzle. A convex quadrilateral is inscribed in a rectangle with exactly one quadrilateral's vertex on each side of the rectangle. Prove that the area of the rectangle is twice the area of the quadrilateral if and only if a diagonal of the quadrilateral is parallel to two parallel sides of the rectangle.
Now it is time for a solution where I use the sample rectangle pictured below. We draw lines parallel to the sides of the rectangle from every vertex of the quadrilateral. Now, we can find four pairs of congruent triangles where one triangle is inside the quadrilateral and the other is outside. In the picture below, the pairs are colored the same color. We see that green and red rectangles overlap, creating a brown rectangle. The fact that they overlap means that the quadrilateral's area is less than half of the rectangle's area.
It could go the other way, as the next picture shows. Here, the quadrilateral's area is more than half of the rectangle's area. In this case, we have an "underlap" as opposed to an overlap.
Therefore, the quadrilateral's area is exactly half of the rectangle's if and only if there is no overlap/underlap, implying that the thickness of the overlap/underlap rectangle is zero. This means that one of the diagonals of the quadrilateral has to be parallel to two sides of the rectangle.
I recently posted the following polyomino puzzle, and my readers are asking for a solution.
Puzzle. You are given a 5-by-7 rectangle with two corners cut out: A 1-by-1 tile is cut from the bottom left corner, and a 1-by-2 tile is cut out of the top right corner, as pictured. The task is to cut the resulting shape into two congruent polyominoes.
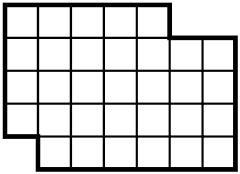
If a solution exists, there should be a transformation between the two congruent pieces. We can exclude a reflection and a central symmetry, as the union of the two shapes would have to be symmetric. We can exclude a translation: I leave it to the readers to explain why. What is left is a rotation or a glide. Let me remind you that a glide is composed of a reflection with respect to a line and a translation parallel to the line.
People often forget about glides, so this puzzle might be cool precisely because it is about glides. This is where we should start. We can safely assume that the top left corner belongs to piece A and, after the glide transformation, becomes the bottom right corner of piece B. It is also clear that the reflection line is parallel to the grid diagonals.
Then, we can start drawing the shapes. Piece A's border starts from the top left corner and moves four squares down, then one square to the right, then one square down. Thus, piece B's border starts at the bottom right corner and continues four squares to the left, then one square up, then one square to the left. In doing so, we reveal how the border of piece A continues. Thus, we can proceed in this manner to get the answer pictured below.

A new geometry problem from my friend, Alexander Karabegov.
Puzzle. A convex quadrilateral is inscribed in a rectangle with exactly one quadrilateral's vertex on each side of the rectangle. Prove that the area of the rectangle is twice the area of the quadrilateral if and only if a diagonal of the quadrilateral is parallel to two parallel sides of the rectangle.
Here is another STEP homework question, which is a famous riddle.
Puzzle. Peter had ten cows. All but nine died. How many cows are left?
The wording is confusing on purpose. So, the students who are in a hurry subtract nine from ten and answer that only one cow is left. This answer is wrong. All but nine means that one cow died. So, the correct answer is nine.
One of my students decided that nine is the name of one of the cows, though it should have been capitalized. This means that all the cows except for Nine died, and only one cow, Nine, is left.
This student managed to find a legitimate explanation for the standard wrong answer.
I love the game of SET, where you have a specialized deck of 81 cards. The image on each card has four features: color, shape, shading, and the number of objects. Each feature can have three possible values. Three cards form a set if, for every feature, the values on the cards are either all the same or all different. One of the best properties of the sets is that, given any two cards, we can calculate the third card that would complete a set.
If we look at the game mathematically, we can assign a number 0, 1, or 2 for every feature value. For example, green could be 0, purple could be 1, and red could be 2. Then, the condition that, given a feature, three cards are either all the same or all different is equivalent to saying that the sum of the values modulo 3 is zero.
A mathematician would wonder, can we make a new game where we take values modulo 4? Each feature value should correspond to 0, 1, 2, or 3. For example, we can add a yellow color corresponding to number 3. The new "set" should be four cards such that the sum of the values modulo 4 is 0. This condition guarantees that any three cards could be uniquely completed into a "set". But such a game is inelegant. For example, one green, two purple, and one red card will form a set. But one green, one purple, and two red will not. The symmetry between colors is lost.
I decided that there is no good analog for the game of SET that is played modulo 4. I was wrong. Here is a new game called EvenQuads. I heard about it at the 2022 MOVES conference.
The deck consists of 64 cards with three features: color, shape, and the number of objects. There are four values for each feature. Four cards form a quad if, for every feature, the values are all the same, all different, or half-and-half.

For example, the figure above shows a quad where, for each feature, all values are different. To get familiar with quads, here is a puzzle for you. How many quads can you find in the picture below?

The game proceeds in a similar way to the game of SET. You can find out more about EvenQuads at the EvenQuads website.
I picked this game as a research project for my senior STEP group. As many of you know, I have a program where we conduct mathematical research with students in grades 7 through 9. The group started in the fall of 2022 and was extremely productive. We wrote FOUR papers in an academic year, which is obviously our record. The papers can be found at the arXiv.
My students did a great job.
I deleted my previous post about Solomon's knot. The reason is simple. I made the mistake of trusting Wikipedia. I was sure that the linking number of Solomon's knot was 2. Then Wikipedia said it was 0, so I fixed "the error" in my post. One of my readers corrected me. So, I rechecked it, removed my post, and fixed the article in Wikipedia. Now, I have a new post about the knot.


Solomon's knot is actually not a knot in a mathematical sense. It is a link because it consists of two loops. It is famous for being one of the simplest linked links. The simplest one is the unlink, the link where two loops are not linked. The next simplest is the Hopf link. The Solomon's knot is the next after that.
Usually, the simplicity of a link corresponds to its crossing number, which is the smallest number of crossings of a projection of the link onto a plane. The unlink has a crossing number of 0, the Hopf link has a crossing number of 2, and the Solomon's knot has a crossing number of 4. However, the linking number created the confusion, so I will explain it.
The linking number is an invariant of a link, which describes how many times one loop goes around the other. It equals zero for the unlink, one for a Hopf link, and two for Solmon's knot.
I often have difficulty calculating the linking number by looking at a picture of a link. This is why I started to crochet links: finding their linking numbers by fiddling with them is easy. The first image shows the crocheted standard representation of Solomon's link. The second image shows the same link, but I slid the red loop so it twists around a small portion of the green loop, which now looks like a segment. Then, I can count the number of times the red loop goes around the green segment. What's important is to keep the direction in mind. In the second picture, one can see that the red loop winds around the green loop twice but in the same direction, making the linking number two.
So far, it looks like the linking number grows with the crossing number. Here is where my favorite link, the Whitehead link, comes in. It breaks the previous pattern. It has the crossing number of 5, so it is slightly more complex than Solomon's link. But its linking number is zero, which is unusual for a linked link. In fact, the Whitehead link is the simplest linked link with the linking number zero, but I already wrote about it in my post Whitehead Links for Ukraine.
Puzzle. A group of 20 students formed a line to take an oral exam with Professor Chill. They were afraid to enter the classroom, so they decided to do a drawing. They wrote the numbers from 1 to 20 on pieces of paper, placed them in a hat, and each student picked one. The student who drew the number 1 went into the classroom first. Then, the remaining 19 students repeated the process, writing down numbers from 1 to 19, and the one who drew the number 1 took the exam next. They continued this process until all 20 students had taken their exams. Remarkably, each student drew a different number each time. Olga drew number 14 in the first round. How many students took the exam before she entered the classroom?
Konstantin Knop posted the following puzzle on Facebook.
Puzzle. An agent sends messages to the command center. The messages have to be encrypted as a stream of 512 characters that can only be zeros and ones. Unfortunately, his transmitter is malfunctioning and gobbles 16 characters of each message. The missing 16 characters are always in the same positions in any message. As a result, the command center receives a sequence of 496 bits. Neither the center nor the agent knows which 16 bits of the sequence are eaten up by the device.
They cannot replace the broken transmitter. However, they can agree ahead of time to send K test messages, the content of which they both know. Find the smallest possible K needed to determine the positions of the disappearing 16 bits.
A quine is a computer program which takes no input and produces a copy of its own source code as its only output.
Puzzle. Assuming English is a computer language, write a quine in English.
My students had many solutions on how to solve this puzzle. They were all variations on "Write this sentence." This is a self-referential sentence which doesn't quite work. I even tried it on ChatGPT with the following result, "Of course, I'd be happy to help! Please provide the sentence you'd like me to write, and I'll assist you with it."
However, the solution I originally had in mind worked. ChatGPT repeated my input. So, ChatGPT provides a simple way for you to check your answer to this puzzle.
My students had more ideas. One of them suggested screaming at a friend, forcing the friend person to scream back. In a similar vein, one might say hello to a person in order to hear hello back. I tried this with ChatGPT, but it didn't work. The bot replied, "Hello! How can I assist you today?"
Another trivial idea is to write nothing. This certainly works perfectly with ChatGPT.
What's a polyomino? A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. Here, we have a puzzle about a polyomino that is almost a rectangle.
Puzzle. You are given a 5-by-7 rectangle with two corners cut out: A 1-by-1 tile is cut from the bottom left corner, and a 1-by-2 tile is cut out of the top right corner, as in the picture. The task is to cut the resulting shape into two congruent polyominoes.

Here's another brainteaser from my friend, Alexander Karabegov.
Puzzle. Place the numbers from 1 to 8 at the vertices of a cube so that each face is balanced. On a balanced face, the sum of the numbers at the ends of one diagonal equals the sum of the numbers at the ends of the other diagonal.
My friend, Alexander Karabegov, sent me one of his puzzles. I love the mixture of algebra and calculus.
Puzzle. Describe a real quadratic function f such that the graph of its derivative f′ is tangent to the graph of f.
My former student, Xiaoyu He, invented this elegant puzzle and shared it with me.
Puzzle. We've got a murder mystery on our hands. There are four suspects, and it's pretty clear that one of them is the actual murderer. But here's the twist: there are also four witnesses who know who the killer is. Now, three of these witnesses are the honest type, always telling the truth, but the fourth one always lies.
You get to ask each of these witnesses a single yes-or-no question, and your question must be, "Is the murderer among this group of suspects?" You can choose any group of suspects you want. The challenge is to figure out who the murderer is.
Can you take it up a notch and determine the murderer if you have to list all your questions before getting any of the answers?
The Museum of Mathematics organizes a biannual conference in recreational mathematics called MOVES: Mathematics Of Various Entertaining Subjects. Being a math-recreatinalist myself, I attend all of them. The last one was held in August 2023 and was devoted to the mathematics of Fiber Arts. A few years ago, I wouldn't have believed I had something to do with the arts. However, in recent years, I started crocheting mathematical objects for my classes, so I not only decided to attend, but also submitted a talk proposal.
The talk proposal was accepted. And, when I finished my slides, I realized that I created too many objects for a 25-minute talk. So, I divided my talk into seven sections and asked the audience to choose. I was lucky that they chose what I was most excited about, but I only had time to cover 4 out of 7 section.
Today I am posting a couple of pictures from my slides that showcase Brunnian links.

A Brunnian link is a set of loops that can't be separated, but if any one loop is removed, they all fall apart. The most famous example of a Brunnian link is Borromean rings which I already wrote about. In the first picture, the Borromean rings are on the right. They are famous because they are the simplest Brunnian link.
There are two natural ways to generalize Borromean rings. One way is to use the same three loops, but make them twist around each other more. The second way is to increase the number of loops.
The left side of the first picture shows three tangled loops, which are more intertwined than Borromean rings. The crossing number of the link on the left is 12, while the crossing number of the Borromean rings is 6.
The second picture shows two Brunnian links with more than three loops. The left link has four loops, while the right link has five.

* * *
—What's the best way to get a math tutor?
—An add!
* * *
—Why was the equal sign so humble?
—Because she knew she wasn't greater than or less than anyone else.
* * *
—Where do mathematicians go on vacation?
—Times Square.
* * *
—Why do cheapskates make good math teachers?
—Because they make every penny count.
* * *
—Why was math class so long?
—The teacher kept going off on a tangent.
* * *
—What did the student say about the calculus equation she couldn't solve?
—This is derive-ing me crazy!
* * *
—Did you hear about the statistician who drowned crossing a river?
—It was three feet deep, on average.
* * *
—What do organic mathematicians throw into their fireplaces?
—Natural logs.
* * *
—Why is the obtuse triangle always upset?
—It is never right.
* * *
—What is the integral of one divided by a cabin? A log cabin?
—No, houseboat — you forgot the C.
* * *
—What do you get when a bunch of sheep hang out in a circle?
—Shepherd's pi.
* * *
—What do you call a metric cookie?
—A gram cracker.
* * *
—What state has the most math teachers?
—Math-achusetts.
* * *
—What does a hungry math teacher like to eat?
—A square meal.
* * *
—What is the mathematician's favorite season?
—Sum-mer.
* * *
—What adds, subtracts, multiplies, divides, and bumps into light bulbs?
—A moth-ematician.
* * *
—What tools do you use for math?
—Multi-pliers.
* * *
—Why didn't the quarter roll down the hill with the nickel?
—Because it had more cents!
* * *
—Which snakes are good at math?
—Adders.
* * *
—What is the butterfly's favorite subject in school?
—Moth-ematics.
The Ural Math Battle in 2016 had several mafia-themed problems of various difficulty with the same initial setup.
Puzzle Setup. Among 100 residents of Saint-San, m are mafiosi, and the rest are civilians. A commissioner arrived to the town after getting this information. In an attempt to expose the mafia, this commissioner asked each of the residents to name s mafia suspects from among the other 99 residents. The commissioner knows that none of the mafiosi would name other mafiosi, but each civilian would name at least k mafia members. What is the maximum number of mafia members the commissioner can definitively identify after his survey?
When I asked ChatGPT to translate the first and the most difficult case of this puzzle from Russian, ChatGPT decided to solve it too. At the end of its ridiculous solution, it concluded that the commissioner could identify all 21 mafiosi out of the given 3. So, if you comment on this blog that the answer to the first case is 21, I will know that you are a bot.
I recently saw another puzzle on Facebook, a generalization of a problem from the 2002 Belarus Olympiad. In the problem, there are red and white boxes. Given how Russia and Belarus are filled with propaganda, my first question was whether the Belarusian flag was red and white. But in fact, the official flag is red and green; however, the opposition uses a red and white one. It could either be a coincidence or a sneaky way of protesting. Anyway, here is the problem.
Puzzle. There are two boxes filled with candy. The red box has R candies, and the white box has W candies. Alice and Bob are playing a game where Alice starts, and both players have the same options each turn: Either move one candy from the red box to the white box or take two candies from any box and eat them. The player who can't move loses. For which values of R and W is each of the following true?
- Alice, following her optimal strategy, wins but might lose if she makes a mistake.
- Alice wins no matter what.
- Bob, following his optimal strategy, wins but might lose if he makes a mistake.
- Bob wins no matter what.
The list of options is weird, but I decided to keep it to emphasize …. Oops, I do not want to spoil it. You can decide for yourself what I wanted to emphasize.
Recently, I decided to stop avoiding puns and childish math jokes. So I am posting a lot of famous jokes I have heard before but never added to my collection.
* * *
—What are ten things you can always count on?
—Your fingers.
* * *
—Why should you never mention the number 288?
—Because it's two gross.
* * *
—Why did the two 4's skip lunch?
—They already 8!
* * *
—How do you make one vanish?
—Add a "g" to the beginning.
* * *
—Why was 6 afraid of 7?
—Because 7 8 9.
* * *
—How do deaf mathematicians communicate?
—With sine language.
* * *
—Why don't math majors throw house parties?
—Because it's dangerous to drink and derive.
* * *
—What's the official animal of Pi day?
—The Pi-thon!
* * *
—What do you get when you take the sun and divide its circumference by its diameter?
—Pi in the sky.
* * *
—Who's the king of the pencil case?
—The ruler.
* * *
—Why was the inchworm angry?
—He had to convert to the metric system.
I've been collecting math jokes for many years, but I was avoiding puns, mostly because of my English. Puns are among the most difficult things to master in a language. Here are some punny jokes that I finally understand.
* * *
—Who invented the Round Table?
—Sir Cumference.
* * *
—Why didn't the hyperbola feel sick?
—It was asymptote-matic.
* * *
—Which triangles are the coldest?
—Ice-sosceles triangles.
* * *
—What's the one shape you should avoid at all costs?
—A TRAP-ezoid.
* * *
—What do you call more than one L?
—Parallel.
* * *
—What do you call a number that can't keep still?
—A Roamin' Numeral.
I was browsing my analog archives, my high-school notes, and stumbled upon a couple of problems from a math battle we had.
Puzzle. A square is divided into 100 pieces of the same area, in two ways. Prove that you can find 100 points such that each piece in the first division has a point inside, and each piece in the second division also has a point inside.
Puzzle. There is a finite number of points on a plane. All distances between any pairs of points are distinct. Each point is connected to its closest neighboring point. Prove that each point is connected to no more than 5 points.

Why would I complicate my life by crocheting colored borders onto different strips?
Answer: I wanted to emphasize their borders.
Do you recognize the objects in the picture? The leftmost one is a Möbius strip. I made it by crocheting a long rectangle. Then, instead of connecting the short sides to form a cylinder, I twisted one side 180 degrees before stitching them together. For the other two objects, I made 360 and 540 degree twists, respectively.
I used green yarn for the internal part of the strips. When the twist in the strip is a multiple of 360 degrees, the resulting surface is orientable and has two borders. I used two different colors to emphasize this fact. In other cases, the resulting surface is not orientable and has only one border, so I only used one color for the border.
The point of using extra colors for the borders is to make them more prominent. For example, it is easy to see that the Möbius strip's border is a circle. The border of the piece in the middle consists of two loops, and the different colors make it obvious that the two borders are linked. The last object has one border, and the color helps you notice that its border is a trefoil knot!
What would happen with the borders if we increase the number of degrees in a twist? Can you figure it out? Are you willing to take up crocheting to solve this puzzle?
* * *
A math problem is the only place where a person buys 7744 watermelons for dinner, but no one knows why!
* * *
Today I saw a tweet from someone I knew in middle school. He tweeted, "I turned my life around 360 degrees!" Now do you see why it is important to study math?
* * *
Looking for energy? Multiply time by power!
* * *
The mom of a third grader calls her friend, "Lucy, did you do your son's math homework?"
"I did."
"Can I copy your answers?"
* * *
If money is measured in piles, then I have a pit.
* * *
My girlfriend is the square root of −100. She's a perfect 10, but purely imaginary.
* * *
A mathematical collapse: while cutting a worm, you divide it by 2 and multiply it by 2, simultaneously!
I used to love math problems about weighing things. But then I got distracted by my own personal scale with its slowly rising numbers. However, having recently lost a few pounds, I want to get back to other scales!
Puzzle. You have a balance scale that is broken in a consistent way: if you put two objects on its two pans, the scale will show you that the left pan is heavier, lighter, or the same weight as the right pan, but it may be wrong. However, it will give the same answer each time you repeat this test with the same two weights. You have a bag of flour and a 1-kilo weight. How can you use this scale to measure out 1 kilo of flour?
Puzzle. This time, your scale is not broken, and, moreover, it is not a balance scale but a digital one that tells you the weight of the objects you put on it. The scale does have a quirk. It can only measure two objects at a time. You have 13 coins of potentially different weights. How can you figure out the total weight of the 13 coins in 8 measurements?
The next puzzle was sent to me by Konstantin Knop, a coin puzzle master. This time there is no physical scale involved; rather, some sort of god answers your questions.
Puzzle. 26 identical-looking coins are arranged in a circle. Two of the coins which are next to each other are fake. You are allowed to pick any set of coins and ask how many fake coins are in the set. What is the smallest number of questions you need to find both fake coins if you only get the answers after you have posed all your questions?

A link is defined as two closed curves in three-dimensional space. The first picture shows an example of a link with one yellow curve and one blue. The linking number is a simple numerical invariant of a link. Intuitively, it represents the number of times that each curve winds around the other. For example, if it is possible to pull the two curves apart, the linking number is zero.
When I studied the linking number, I would look at a picture of a link trying to calculate this number. It was confusing. It only became easy after I started crocheting. For example, the second picture shows the same link as the first but slightly rearranged. I simply slid the yellow loop along the blue one until I could clearly see a piece of the blue loop as a straight segment and the yellow loop circling around it. Now, it is easy to see that the yellow loop winds around the blue one 3 times, making the linking number 3.
The only thing to remember is that while counting the number of windings, I need to consider the direction. It is possible for a loop to wind clockwise and then counterclockwise. In this case, the linking number is the difference between the two.
I crocheted a lot of links, and now my students and I have no problem calculating the linking numbers.

In December 2022, I wrote a blog post Uncrossed Knight's Tours about Derek Kisman's amazing achievement of calculating the largest uncrossed knight's tours on rectangular chessboards on sizes M-by-N, where M is small, and N can be very very large.
The data showed some asymptotic periodicity, and I wondered how to prove it mathematically. I didn't realize that Derek already proved it. In my ignorance of programming, I assumed that programs just spewed out the data and didn't think they could prove anything. I was wrong. It appears that no other proof is needed. Derek tried to explain the details to me using the terminology of dynamic programming, but I am not sure I can reproduce it here.
Let's recall the problem. Consider an M-by-N chessboard and a knight that moves according to standard chess rules: jumping one square in one direction and two squares in an orthogonal direction. The knight must visit as many squares as possible, without repeats, and then return to its starting square. In addition, the knight may never cross its own path. If you imagine the knight's path consisting of straight line segments connecting the centers of the squares it visits, these segments must form a simple polygon. To summarize, given M and N, we want to calculate the longest uncrossed knight's tour length.
To be clear: the programs, their output data, proven answers, and images are by Derek Kisman. I am just a humble messenger showing my new appreciation of the power of a computational proof.
The image shows Derek's solution for a 3-by-13 chessboard. There is a repeating 3-by-4 pattern marked by dashed lines. The same tour works for boards of lengths 10, 11, and 12. Thus, for chessboards of width 3 and length from 10 to 13 inclusive, the longest uncrossed knight's tour is length 10. We can write the answers for 3-by-N chessboards as a sequence with index N, where -1 means the tour is impossible. The sequence starts with N = 1: -1, -1, -1, 4, 6, 6, 6, 6, 10, 10, 10, 10, 14, 14, ….
We can prove that this sequence is correct without programming. Suppose the tour starts in the leftmost column. If we start in the middle of the column, the whole tour ends as a rhombus and a tour of length 4, which, by the way, is the longest tour for N = 5. Thus, for a larger N, we have to start in a corner. From there, there are only two possible moves. We can see that the continuation is unique and that, asymptotically, we gain one step per extra column. That is, asymptotically, the length of the longest tour divided by N is 1.
Derek uses an additional notation in the following sequence: each cycle is in brackets. Any two consecutive cycles differ by the same constant. So to continue the sequence indefinitely, it is enough to know the first two cycles.
Closed tours: 3xN (asymptote 1): -1, -1, -1, -1, 4, [6, 6, 6, 6], [10, 10, 10, 10], ...
I continue with other examples Derek calculated:
Closed tours: 4xN (asymptote 2): -1, -1, -1, [4], [6], ...
Closed tours: 5xN (asymptote 2 3/5): -1, -1, 4, 6, [8, 12, 14, 18, 20, 22, 24, 28, 30, 34], [34, 38, 40, 44, 46, 48, 50, 54, 56, 60], ...

Closed tours: 6xN (asymptote 4): -1, -1, 6, 8, 12, 12, 18, 22, 24, 28, 32, 36, [38], [42], ...
Closed tours: 7xN (asymptote 4 10/33): -1, -1, 6, 10, 14, 18, 24, 26, 32, 36, 42, 44, 48, 54, 58, 62, 66, 72, 74, 80, 84, 88, 94, 98, 100, 106, 112, 114, 118, 124, 128, 130, [136, 140, 144, 148, 154, 158, 162, 166, 170, 176, 180, 184, 188, 192, 196, 200, 204, 210, 214, 218, 222, 226, 232, 236, 240, 244, 248, 254, 256, 260, 266, 270, 274], [278, 282, 286, 290, 296, 300, 304, 308, 312, 318, 322, 326, 330, 334, 338, 342, 346, 352, 356, 360, 364, 368, 374, 378, 382, 386, 390, 396, 398, 402, 408, 412, 416], ...

Closed tours: 8xN (asymptote 6): -1, -1, 6, 12, 18, 22, 26, 32, 36, 42, 46, 52, 58, [64, 70, 76, 80, 88, 92], [100, 106, 112, 116, 124, 128], ...
Closed tours: 9xN (asymptote 6 6/29): -1, -1, 6, 14, 20, 24, 32, 36, 42, 50, 56, 60, 68, 74, 80, 86, 94, 98, 106, 114, 118, 126, 132, 136, [144, 150, 156, 162, 168, 174, 180, 186, 192, 200, 206, 212, 218, 224, 230, 236, 242, 250, 254, 262, 268, 274, 280, 286, 292, 300, 304, 312, 318, 324, 330, 336, 342, 348, 354, 360, 366, 372, 378, 386, 392, 398, 404, 410, 416, 422, 428, 436, 440, 448, 454, 460, 466, 474, 478, 486, 492, 498], [504, 510, 516, 522, 528, 534, 540, 546, 552, 560, 566, 572, 578, 584, 590, 596, 602, 610, 614, 622, 628, 634, 640, 646, 652, 660, 664, 672, 678, 684, 690, 696, 702, 708, 714, 720, 726, 732, 738, 746, 752, 758, 764, 770, 776, 782, 788, 796, 800, 808, 814, 820, 826, 834, 838, 846, 852, 858], ...

Closed tours: 10xN (asymptote 8): -1, -1, 10, 16, 22, 28, 36, 42, 50, 54, 64, 70, 78, 84, 92, 100, [106], [114], ... I do not have an image for this case.
As you might have noticed, for an even M, the asymptote equals M-2. The asymptote for an odd M is slightly greater than the asymptote for M-1.
Derek also calculated the longest open knight's tours: the tours where the knight doesn't have to return to its starting position.
Open tours: 2xN (asymptote 1/2): -1, -1, [2, 2], [3, 3], ...
Open tours: 3xN (asymptote 1): -1, 2, 3, 5, 6, 7, [9], [10], ...
Open tours: 4xN (asymptote 2): -1, 2, 5, [6], [8], ...
Open tours: 5xN (asymptote 3): -1, 3, 6, 8, 11, 15, 17, 20, 23, 26, 29, [32, 35, 38, 41, 44, 46], [50, 53, 56, 59, 62, 64], ...
Open tours: 6xN (asymptote 4): -1, 3, 7, 10, 15, 18, 22, 26, 30, 33, [36], [40], ...
Open tours: 7xN (asymptote 5): -1, 4, 9, 12, 17, 22, 25, 31, 36, [40], [45], ...
Open tours: 8xN (asymptote 6): -1, 4, 10, 14, 20, 26, 31, 36, 43, 48, 54, 60, [64], [70], ...
Open tours: 9xN open (asymptote 7): -1, 5, 11, 16, 23, 30, 36, 43, 48, 56, 62, 68, 75, [82, 88, 94], [103, 109, 115], ... I do not have an image for this case.
There are a lot of interesting new sequences in this essay that were very nontrivial to calculate. I hope someone adds them to the OEIS database.
I stumbled upon a cute puzzle on Facebook which originally came from a new book, Creative Puzzles to Ignite Your Mind by Shyam Sunder Gupta.
Puzzle. We have four identical boxes. One of the boxes contains three black balls (BBB), another box has two black and one white balls (BBW), the third box has one black and two white balls (BWW), and the last box has three white balls (WWW). Four labels, BBB, BBW, BWW, and WWW, are put on the boxes, one per box. As is often the case in such puzzles, none of the labels match the contents, and this fact is common knowledge. Four sages get one box each. Each sage sees his label but doesn't know the other's labels. Without looking in the box, each sage is asked to take out two balls and guess the color of the third ball. All the sages are in the same room and can hear each other and see the colors of the balls that are taken out.Can you figure out what's in the boxes?
- The first sage takes out two black balls and says, "I know the color of the third ball."
- The second sage takes out one black and one white ball and says, "I know the color of the third ball."
- The third sage takes out two white balls and says, "I don't know the color of the third ball."
- The fourth sage says, without taking out any balls, "I know the color of all the balls in my box and also the content of all the other boxes."
After I crocheted Whitney Umbrellas, I got excited that I figured out how to crochet through an existing layer of fabric. I decided to use my skills to crochet "correct-er" Klein bottles.
A Klein bottle is a cool mathematical surface with only one side, similar to the Möbius strip. Unlike the strip, the Klein bottle has no border making it a non-orientable manifold. The problem in making Klein bottles is that the Klein bottle can't be embedded into 3D space. Thus, all 3D models of Klein bottles have to self-intersect. But all the models that I saw, including glass models and crocheted hats that you can buy at ACME Klein Bottle, have holes.


I realized that my method of crocheting through might allow me to make more accurate models of Klein bottles, ones without holes.
Now it is time to spill my secret. The idea is easy, the implementation is not. The two pictures show the same yellow cylinder crocheted through a green square, viewed from different angles. I crocheted the green square first, then half of the yellow cylinder. Afterwards, I had to pull the whole ball of yellow yarn through a tiny hole in the middle of the green square. Then, with my hook, I pulled each yellow stitch from one side of the green square to the other side through its own tiny hole and finished the stitch on the new side. In the third picture, you can see my Klein bottle made in two colors. You might be able to see the second color inside instead of a hole.


I invented this method while crocheting Whitney's umbrellas. I had to pull the whole ball of yarn through a tiny hole once per row. I still remember the tediousness of it with dread.
After the bottles, I decided to try projective planes. In the fourth picture, you can see two projective planes and two projective planes with holes. For the former, I started with the bottom hemispheres, and for the latter with cylinders. I didn't need to crochet through or pull yarns through tiny holes. I just crocheted one row across the other. I left the easiest crochet task for last!
I do not like odd-one-out puzzles. This old and famous example is one of the reasons why. When given the list: skyscraper, cathedral, temple, and prayer, people usually pick "prayer" as the odd-one-out because it's not a building. On the other hand, when the order is prayer, temple, cathedral, and skyscraper, people would pick "skyscraper" as it is not related to religion.
I created several pairs of questions that might have a similar issue: the answer depends on how the list is ordered.
Odd-one-out dilemma. Pick the odd-one-out from:
- Pen, book, notebook, tissue.
- Tissue, notebook, book, pen.
Odd-one-out dilemma. Pick the odd-one-out from:
- Banana, apple, orange, grape, lime, nectarine, artichoke.
- Artichoke, nectarine, lime, grape, orange, apple, banana.
Odd-one-out dilemma. Pick the odd-one-out from:
- 6, 3, 15, 9, 5.
- 5, 9, 15, 3, 6.
I buy almost everything on Amazon. Recently, I ordered a back stretcher. It took half an hour to assemble, and after the first use, it changed shape. However, this story is not about quality but about a card that was included with the item.
In the box, I found a gift card that wasn't a gift card but rather a promise of a $20 Amazon gift card for a 5-star review. Hmm! A bribe for a good review.
I looked at the card more closely, and it had the following text.
WARM TIPS: Please DO NOT upload gift card pictures in the review; it will affect your account.
This is not only a bribe. It contains a threat.
Initially, I assumed it was Amazon, but it makes more sense that the company making this thingy is behind it. I gave Amazon the benefit of the doubt and went to their website to leave a 1-star review. I related the card's story to warn others that the 5-star reviews can't be trusted. Amazon rejected my review as it didn't comply with their guidelines. Is Amazon in on it?
I wrote a different 1-star review, which did comply. It seems I can complain about the product, but I can't complain about the bribe and threat.
I called Amazon's customer service, and they promised to investigate. This was three months ago. This crappy product, with a stellar average 4.6 rating, is still out there.

* * *
The teacher asks a student,
"Johnny, how much will your mom pay at the market for three pounds of apples if one pound is three dollars?"
"I do not know," answers Johnny, "My mom loves bargaining, and she is good at it."
* * *
The teacher asks a student,
"Johnny, in a 5-story building, you have to go up 30 stairs to get from one floor to the next. If you go from the first to the fifth floor, how many stairs do you have to take?"
"All of them," answers Johnny.
* * *
The teacher asks a student,
"Johnny, you have 10 dollars in your pocket. You ask your dad for 10 more. How much money will you have?"
"I will have 10 dollars."
"You do not know your math!"
"You do not know my dad!"
I am sure I was fooled many times on April Fool's Days. But I do not remember any stories, except one. It was quite painful and had a lot of potential for humiliation.
I was in high school, and our school didn't have enough rooms for all the classes. So that particular semester, our classes happened during the second shift: from 2 pm to 8 pm.
One day, I received a call from my friend that school was canceled the following day. My friend told me that I had to notify half of the class. We had about 40 students in our class. She would call everyone whose last name started with the letters A through N, and I would have to call everyone else.
To set the stage, I was really, really shy. Calling people was torture. On the other hand, I was a very responsible person. So, I was walking in circles around our family's phone with my hands shaking. Then, suddenly, a light bulb went off in my head: the day was April 1st.
It was a great excuse: if I told people not to come to school, they might not believe me. Hooray! I can procrastinate until the next day. Because we wouldn't start until 2 pm, I would have enough time to notify everyone in the morning.
When I woke up the next day, the other light bulb went off: I didn't need to call anyone; but I definitely had to have a chat with my "friend."
I am deeply fascinated with my family's history, so I took it upon myself to enlighten my children about our family tree. One day my son retorted, "This is not a family tree; this is a family bush."
He was right. I was married three times and had a child from two of my three husbands. My ex-husbands had other children. So our family "tree" branches out in chaotic and weird ways.
My two sons are half-brothers, and each of them has other half-siblings. With mathematics all around them, my sons decided to quantify their family connections: they named a half-sister of a half-brother a quarter-sister.
I didn't have any children with my first husband, Alexander. But he remarried after our divorce and had two children. I've never met Alexander's offspring, but my children hang out with them. Go figure! This is not just because the world is too small; rather, my exes are mathematicians and work with each other. So, theoretically, if Alexander and I had a common child, Alexander's children would have been quarter-siblings to my sons. In real life, we didn't have a child. Still, can my sons call Alexander's children virtual quarter-siblings?
My new logic puzzle happens in the usual place: an island with truth-tellers and liars. Truth-tellers always tell the truth, while liars always lie. The liars on this island are dedicated to their lies: they do not want other people to figure out that they are liars and want to confuse people with their responses as much as possible. They also are cooperative: they coordinate their answers. The islanders all know each other and who is who.
Puzzle. A stranger arrives on this island with a plan. Each time the stranger hangs out with a group of people, he will ask each person the same question:
How many truth-tellers are in this group?The liars on this island discover the stranger's plan, and, being cooperative and dedicated, they do not want the stranger to figure out the true answer to his question. They also do not want the stranger to know anyone's identity. What should they say?
For starters, any dedicated liar should always provide a theoretically possible answer. The liar shouldn't say, "three quarters" or "infinitely many", as these are obvious lies. In addition, the answer "zero" is too revealing: a truth-teller would never say this. Thus, the liar would answer with a positive integer that doesn't exceed the total number of people in the group.
Suppose, for example, the stranger meets three people. Then there could be 0, 1, 2, or 3 truth-tellers in the group. As we discussed before, everyone replies 1, 2, or 3.
If there are t truth-tellers in the group, then the answer t is repeated exactly t times. That means the following sets of three answers reveal that all three islanders are liars: {1,1,1}, {1,1,2}, {1,1,3}, {2,2,2}, and {2,3,3}. With the following sets of answers, the stranger can figure out who is the only truth-teller: {1,2,3} and {1,3,3}. The set {2,2,3} allows the stranger to find both truth-tellers. And the following sets of answers do not allow the stranger to figure out who is who: {1,2,2} and {3,3,3}. So those sets of answers are the ones the liars will choose.
To sum up, the best strategy is for all the liars in the group to answer x, where x is the number of liars. Meanwhile, all the truth-tellers would say: 3 − x. That way, the stranger cannot differentiate between the truth-tellers and the liars.
The strategy above works with a group of any size as long as the number of liars is not equal to the number of truth-tellers.
Bonus Puzzle. Is there a way to confuse the stranger when the liars make are half of the group?
Another gem posted by Konstantin Knop on Facebook.
Puzzle. The Vicious Dragon captured two princesses, Evangelina and Oddetta, and placed them in different towers in his castle. Then the Vicious Dragon flipped a fair coin an infinite number of times. He informed Evangelina of all the results of the even tosses and Oddetta of all the results of the odd tosses. Next, the Dragon asks each princess to name the number of any toss whose result is unknown to her. In other words, Evangelina must name an odd number, and Oddetta must name an even number.
If the tosses named by Evangelina and Oddetta are the same (both are tails or both are heads), the Vicious Dragon gives each princess a cake and a pink plush bunny and sets them free. But if the results differ, the Vicious Dragon devours Evangelina and Oddetta with cranberry jam. The Dragon loves princesses and cranberry jam!
The princesses know the Vicious Dragon's habits and could have agreed on strategies in advance. What are the chances of the princesses escaping if Oddetta names a number first, and Evangelina names her number, knowing which number Oddetta chose?
Puzzle. Alice and Bob roll an unbiased 6-sided die until two consecutive rolls are the same. They add up the scores from all of the rolls. If the total is even, Alice wins; if it is odd, Bob wins. Who is more likely to win?
My son, Alexey Radul, designed a puzzle for my students.
Puzzle. Simplify the expression: ln ln a · ln ln b · ⋯ · ln ln z.
Every year, I used to blog about math-related puzzles from that year's MIT mystery hunt. However, I want to skip this year. I participated in the hunt, and a few of the puzzles I saw were not good enough. Moreover, the puzzles had boring steps or were inelegant. I am not motivated to sift through every math puzzle in the hunt and check its quality.
This year, instead of cataloging all the math puzzles, I will present a short list of puzzles from the hunt that were recommended to me by others. Most of these puzzles are unrelated to math, but I checked them out, and they seem cool.
After the hunt, I asked two people about their favorite puzzles. Both of them mentioned Showcase. Looking at it, I know why. I'll give you a hint: this puzzle will appeal to people doing competitive programming.
Here are some other recommendations.

Puzzle. If you can move exactly two matches, what is the largest possible number you can get?
Many people assume that given that 508 has three digits, the answer also has three digits. They get the number 999 and stop there.
Some students realized they can make an extra 1 out of two matches and gave answers with four digits: 1503, 5051, and 5103.
Another great idea is to take out the two horizontal matches from 0, turning the 0 into 11. For example, one might use the two matches to turn 5 into 8 and get 8118. However, we can combine this idea with the previous one and use the two matches to make a new digit 1 to get 51181.
When I first saw this puzzle several years ago, 51181 was the official answer. But my students went further, much, much further.
Another elegant idea is to rotate the picture and get 81151.
Some students decided that having all the digits be the same height is not very important. One vertical match reads as 1, even if it is half the height. The largest number they got this way was 511811. Combining this idea with flipping the number allows us to get 811511.
However, small-font digits are often used in powers. This train of thought led to a brilliant answer, 511811. This number is way larger than everything we saw before: it has 41 digits. If we combine this idea with rotating the number, we can get 811511, a 43-digit number.
I recently decided to check the Internet again and discovered a chain of videos showing solutions to this puzzle by the same author. He started with a simple solution, 51181, then people left comments in the video with better solutions, so he remade the video. This happened several times. I probably should send him a link to this essay for yet another video.
Here is an interesting solution by one of my students that I haven't seen anywhere else. The idea is to use scientific notation. The student took two matches from the right side of 0. He used one of them to convert the first digit from 5 to 9 and the second digit from 0 into the letter E. He got 9E8 = 900000000. If we combine this idea with using a small 1, we can get 5E81, an 82-digit number.
Another brilliant idea is using two matches to create a caret symbol representing an exponent. This way, we can get 5^118, which is an 83-digit number. If we combine this idea with the rotation idea, we can get 8^115, a 104-digit number.
If we ignore the relative sizes of the digits, we can have the small digits as the base of the exponent and the larger digits as the power. One of the students suggested 115118, a 5330-digit number. And if we rotate the number, the answer we can get is 118115: the number with 8451 digits. This is a humongous number compared to the mere 3-digit one we started with, to the pathetic 5-digit original solution, and to the pitiful 104-digit previous record. But my students didn't stop there.
One student suggested snapping two matches and creating a double factorial 505!!, with 575 digits. Combining this with other ideas, we can get 8115!!, a 14102-digit number.
One of my students decided to use two matches from the last digit 8 to create a factorial sign. She glued one of the matches perpendicular to the plane to get 505! in the projection. She even made a picture that you can see below. This number has 1148 digits, and combining this with previous ideas, we can get 5118!, which has 16763 digits. Or even 8115!, which has 28202 digits.

For this puzzle, a factorial works better than a double factorial. Here is my own suggestion: use one of the matches to create a small digit one, and split the other match into a factorial. This way, we can get 81151!, a number with a whooping 363154 digits.
This is an excellent example of a thinking-outside-the-box puzzle. I love this puzzle because it has not one, but many boxes one can think outside off.
Sometimes I mess with my students. Recently, I gave them the following problem for homework.
Puzzle. Don't read this sentence.
This problem is a paradox: students can't know not to read it unless they read it! I expected my students to explain the paradox, and a couple of them did. But, most of them provided me with an infinite stream of entertainment. Here are some of their answers divided into categories, starting with the apologizing ones, and there were a lot of those:
I wasn't surprised by the apologies, as this problem is intended to be intimidating. However, other students tried to wiggle out of it:
Yet other students decided to rebel:
Karma is a boomerang, and this problem got me into a pickle. One of the most brilliant and funny solutions possible was to leave the answer box blank, implying that the sentence wasn't read. However, how would I grade this? What if they just skipped the problem? I decided to err on the students' side and gave full credit for an empty answer box.
A couple of students made a point of pretending they didn't read the sentence:
But I saved the best for last. My favorite answer was the following:
Puzzle. Alice and Bob play the following game on a regular chessboard, where all the pieces move according to the standard rules of chess. Alice has a king, and Bob has a knight. They would place their pieces on the chessboard without attacking each other. Alice starts, and they alternate moves. Alice loses if the knight checks or all available moves place her under the knight's attack. For which initial positions of the pieces is Bob guaranteed a win?
Once, I was in Princeton and attended a lecture by Persi Diaconis. John Conway was also there. During his presentation, Persi mentioned John by referring to him as Wonderful John Conway. John couldn't resist and said, "Thank you, you are one of not many people who remember my real first name."
Every summer when I was little, my mom would take us on vacation to a rusty village far away from Moscow. I do not remember much, mostly just cows grazing on the grassy fields. However, one particular memory is really special and vivid.
I was five years old, tired of another day in the fields, lying in bed about to fall asleep. I started counting. I do not remember what. I am sure it wasn't sheep; it could have been cows. Then, I got bored of small numbers and jumped to a thousand, counting from there. Then, I jumped to another even bigger number. After a few jumps, I realized that I could always add one to a previous number. The number of numbers must be infinite. Wow!
I will always remember the feeling I had. It was like touching eternity, being one with the whole universe.
You can imagine why I became a mathematician. From time to time, I am touching eternity and getting paid for the bliss.

I use Escher's tessellations to teach wallpaper groups. Escher is the best painter among mathematicians and the best mathematician among painters. His fame helps energize my class. Plus, he has so many beautiful drawings to choose from.
However, there is another layer to his tessellations. Many paintings are not just a study in wallpaper groups but also in group-subgroup pairs. For example, consider these red/gray/black fishes on the left. There are three distinct points where three different reflection lines intersect. The first point is where three black fishes kiss each other. The other two points correspond to gray and red fish kisses. In orbifold notation, this symmetry group is *333.
But, the same drawing has another symmetry group. We just need to ignore color. That is, we consider all the fishes to be the same. In this case, our three distinct points where three reflection lines intersect become the same point: the point where fishes kiss, regardless of their color. The new symmetry group has an additional element: a 120-degree rotation where three fins of three different-colored fishes touch each other. Thus, the new symmetry group is 3*3.
Escher created a lot of examples of groups and their subgroups using color. But, sometimes, he was more subtle. In one of my previous posts, The Dark Secret of Escher's Shells, I discussed my favorite Escher's plane tessellation. In that drawing, the second group appears when we ignore the markings on one of the dark shells.
Here is another spectacular example of a group and subgroup, a tessellation of a hyperbolic plane with angels and devils. Do you see two different symmetry groups in the painting?

My PRIMES project last year, done with Rich Wang, was about violinists living in a hotel and being annoyed with each other. The project was suggested by Darij Grinberg and based on the following puzzle.
Puzzle. Consider a hotel with an infinite number of rooms arranged sequentially on the ground floor. The rooms are labeled from left to right with consecutive integers. A finite number of violinists are staying in the hotel with no more than one violinist in a room. Each night, two violinists staying in adjacent rooms get fed up with each other's playing, and both request different rooms from the manager. The manager moves one of them to the nearest unoccupied room on the left and the other to the nearest unoccupied room on the right. This keeps happening every night as long as there are two violinists in adjacent rooms. Prove that this relocation will stop after a finite number of nights.
The project was not to solve the puzzle, and I won't describe the solution, leaving it to my readers to ponder on their own. The project was to take this puzzle and see what we could discover. The relocation process in the puzzle is reminiscent of chip-firing, with a few differences.
Let me explain chip-firing in terms of violinists. The starting position would allow any number of violinists per room. Each night, two violinists in the same room will get annoyed with each other and request new rooms. There might be more violinists in that same room, but only two at a time are really annoyed. The manager will put one of them into the room on the left and the other into the room on the right, regardless of how crowded the rooms are.
In the chip-firing example, violinists always move to the next room. In our puzzle, they might need to go miles to a new room. And carry their luggage with them!
The original puzzle above implies that after several nights the relocations will stop, and violinists will enjoy the hotel in peace. This peaceful configuration is called a final state. Interestingly, depending on the order in which violinists are getting annoyed with each other, a starting configuration can result in different final states.
For example, consider the smallest interesting case, where only 3 violinists are staying in a hotel. We use 1 to describe a noisy room with a violinist and 0 to describe an empty room. Suppose the starting configuration is 0011100, where we ignore rooms far away from the noise. Depending on which two rooms have the complaining violinists on the first night, we can end up with a final state 0101001 or 1001010.
Initially, in the project, we looked at final states where we start with N violinists in consecutive rooms. We call such a configuration an N-clusteron. The example above describe the final states of a 3-clusteron. Here is an exercise for the reader: prove that in the final state, the gaps between occupied rooms have to be 1 or 2.
A final state can be described by the index of the leftmost occupied room and the sequence of gaps between occupied rooms. In the exercise above, it is easy to prove that the gaps must be size 1 or 2. In our paper, we proved a more refined statement: any final state has exactly one gap of size 2. Thus, a final state has two parameters: the index of the leftmost room and the location of the size 2 gap. For example, this means that in a final state, the span between the leftmost and the rightmost rooms, inclusive, is 2N.
As we continued exploring final states, we discovered something else. But first, I need to define the shadow of a final state. Let's denote an occupied room with a one and an empty room with a zero. Then a final state corresponds to an infinite sequence of zeros and ones. But the interesting part of the final state is not infinite: it is a subsequence between the leftmost and rightmost ones, inclusive. We call this subsequence the shadow of the final state. In other words, the shadow describes the final state up to a translation and is completely defined by one parameter: the location of the 2-gap. In our example of a 3-clusteron, there are 2 final states with 2 distinct shadows. For larger clusterons, the situation is more interesting. There are 5 different possible final states for a 4-clusteron but only three distinct shadows. We discovered the following conjecture.
Conjecture. If we start from an N-clusteron and at each state uniformly select a move to perform from all possible moves, then the shadows of the final states are equiprobable.
You can find more details in our paper Ending States of a Special Variant of the Chip-Firing Algorithm. This conjecture is beautiful as it shows that there are hidden symmetries in this process of appeasing the fussy violinists. We didn't prove this conjecture. Can you do it?
"Follow your heart!" This is the most common advice for young people contemplating their future career path. This is not good advice. At some point in my life, the most popular aspiration among my friends' children was to become opera singers. But the world only has room for a few opera singers. All of these children ended up doing something completely unrelated.
Aspiring to be a mathematician is a much more practical dream. There are so many professions that are friendly to mathematicians: actuary, finance, economics, teaching, computer science, cryptography, and programming, to name a few. Unlike opera singers, skilled mathematicians can find a way to get paid for their mathematical gifts.
However, most of the youngsters around me want to be research mathematicians. This is a different story. My adviser, Israel Gelfand, told everyone that if they could survive without mathematics, they should drop it. I did drop mathematics for some time to care for my children, but I couldn't live without mathematics. I fed math to my children for breakfast and pursued math hobbies that could fit a single mother's lifestyle. Well, that means I was mostly working with sequences for the Online Encyclopedia of Integer Sequences and building the database for my Number Gossip website. But I digress.
I agree with Gelfand. Research in math as a career choice is non-trivial. Here are some of the big issues:
So what would I suggest for young people who love math?
Many people who love math do not really love math per se. They love the way of thinking that math encourages. They love logic, generating ideas, precision, innovation, and so on. This makes their potential job search much wider. Such people might enjoy programming, cryptography, data science, actuarial science, finance, economics, computer science, engineering, etc. I know students planned to become mathematicians but tried an internship in finance and found their real passion.
For those who want to be closer to mathematics, there is always teaching: the world needs way more math teachers than research mathematicians. Plus, teaching provides a strong feeling of making an impact.
So what do I suggest for young people who love opera singing?
Many skills are less in demand than mathematics. It is important to be realistic. So here is my advice:
I know a former Soviet mathematician who worked as a night guard and used his quiet work time to invent theorems. He was a good mathematician but couldn't find a research position because he was Jewish. He later immigrated to the US and found a professorship. So sometimes my advice for opera singers works for mathematicians too.
Puzzle. "I guarantee," said the pet-shop clerk, "that this parrot will repeat every word it hears." A customer bought the parrot but found it wouldn't speak a single word. Nevertheless, the clerk told the truth. Explain.
The official answer:
Indeed, in this case, it is not a lie that the parrot will repeat every word it hears. My students had some other ideas. The following answer differs from the official one by one letter, but the spirit of the solution is the same.
Another idea my students had was to introduce a time component.
And a couple of outside-of-the-box answers.
Puzzle. Alice and Bob divide a pie. Alice cuts the pie into two pieces. Then Bob cuts one of those pieces into two more pieces. Then Alice cuts one of the three pieces into two pieces. In the end, Alice gets the smallest and the largest piece, while Bob gets the two middle pieces. Given that both want to get the biggest share of the pie, what is Alice's strategy? How much can she get?
Many years ago, I visited a distant country and rekindled my friendship with a nice couple, Alice and Bob. I changed the names and do not remember the exact words. But here is the story.
One evening, I found myself chatting with Bob, and he decided to open up. He told me he was having an affair. After he finished his long story, I asked him whether he thought Alice might also be having an affair. He replied, "It's impossible. She was never a passionate person. And recently, she became even more cold and distant." I didn't follow his logic but didn't pursue the topic.
Several days later, I chatted with Alice, and she decided to open up. She told me that she had met someone and was having an affair. She told me that she never quite enjoyed sex with her husband, but the new guy fitted her perfectly. For the sake of symmetry, I asked her whether she thought her husband might also be having an affair. She replied, "It's impossible. He is too busy at work, and recently, even more so. He goes on business trips twice a week and is always tired."
I invented this puzzle. It's a variation of something I saw on Facebook.
Puzzle. The future dinner of an anthropophagusphagusphagus met for dinner the past study object of an anthropophaguslogist. What's for dinner?
Here is a famous old joke about Russian propaganda. I heard it when Leonid Brezhnev was General Secretary of the Communist Party of the Soviet Union and Ronald Reagan was the president of the US.
Joke. A Russian newspaper wrote an article about a two-person race between the Russian and the US leaders. They wrote, "Brezhnev got an honorable second place, while Reagan was almost last".
Here is a modern version of this joke I heard going around.
Joke. A Russian TV commentator: Biden cowardly goes to war-torn Kyiv, while Putin heroically hides in his bunker.
Before dividing chores, let's divide a cake. Suppose I bought a two-layer cake. One layer is chocolate and the other is vanilla. Suppose I love chocolate and hate vanilla, My friend, Joe, is the opposite: he loves vanilla and hates chocolate. It's very easy to divide the cake. I take all the chocolate, and Joe takes all the vanilla. I think I am lucky to get the full value of the whole cake. Joe feels lucky too.
My point is that people with different tastes can divide things so that both get more than half by their own estimates.
Let's look at another example. Suppose Alice and Bob are divorcing. Their estate consists of one valuable thing: a portrait of Alice's grandfather. Alice loved her grandfather and values the portrait at 10,000 dollars. Meanwhile, Bob values it the same as its market value, 2,000 dollars. There exists a division algorithm, called the Knaster procedure, which allows them to divide the portrait so that both of them end up with the same amount of money on top of their perceived half of the estate.
I will skip the calculations. The end result is that Alice gets the portrait and pays Bob 3,000 dollars. In her view, she gets a portrait worth 10,000 and loses 3,000. Her total gain is 7,000 dollars, which is 2,000 more than her estimated half. Bob gets 3,000 dollars. In his view, half of the estate is 1,000 dollars, and he gets 2,000 more than that.
The bigger the difference in perceived value, the more each person gets in addition to their expected half. Suppose this difference is D. If you trust my calculations, the Knaster procedure means each person gets D/4, in addition to one half of their estate's perceived value.
The same idea can be applied to chores. Suppose I hate shopping while my husband hates doing the dishes. So, I can do the dishes, and he can shop. And we can live happily ever after without doing the things we hate.
So, theoretically, it is very profitable for two people to live together. Have you seen couples where each one thinks that they won the lottery by marrying their partner? Such couples benefit from dividing chores, appreciate their partners' help, and are happy.
I have seen such couples, though not many. Actually, not many at all. If mathematics says that living together should be profitable, then why are happy couples such a rarity?
I will divide unhappy couples into four categories depending on whether they both benefit from dividing the chores and whether they both appreciate each other.
Benefit and appreciate. In this case, other parameters could affect their happiness: love, sex, children, jobs, and so on. Consider, for example, Alice and Bob. Alice relies on her husband for financial support for her and their small children and appreciates said support. Bob likes how Alice cares for the children and appreciates her for that. However, Alice doesn't love Bob anymore, and Bob wants something special in his sex life but is afraid to request it from Alice. They are both profoundly unhappy.
Benefit and do not appreciate. It is possible that both people do not appreciate each other, or it could be just one. In addition, it could be that a person underestimates the real value of the partner's contribution, or it could be that the appreciation is not enough for the partner. This became a more complicated paragraph than I initially expected. As Lev Tolstoy said, "All happy families are alike; each unhappy family is unhappy in its own way." So, let me have two subcases.
Benefit and do not appreciate. Case 1. Underestimation. Such couples have a good division of labor but underestimate each others' contribution. For example, Bob thinks that staying at home with children is a walk in the park. He thinks his job is way more difficult than his wife's daily caring for the house and the children. He assumes that when he returns from work, the house needs to be clean and dinner ready. He is very angry when this doesn't happen. Alice is very unhappy as she knows how much she actually works.
Benefit and do not appreciate. Case 2. No gratitude. Such couples have a good division of labor but do not express their gratitude sufficiently for the other partner. For example, Alice wants Bob to take her out to dinner as a thank you. Or to say thank you on a regular basis. But Bob brags to his friends that he is lucky in marriage and thinks that this is enough. Everyone but her knows that he feels lucky.
Do not benefit. It is usually one person who is used. There are many ways for people to force their spouses to divide the chores in their favor. There are many types of abusive relationships. I do not even want to give an example. After all, my goal was to discuss the mathematics of chores' division, not to analyze why people do not divide their labor fairly.
Special cases. Life is complicated. Here is the case that doesn't quite fit the cases above as the division of chores with time delays. For example, Alice worked and cared for the children while Bob went to medical school. The benefit for Alice was implied in the future. Bob promised to shower her with money when he would get rich. However, as soon as he got rich, he showered someone else.
The mathematics show that living with a partner can be extremely beneficial for both. But people's emotions are complicated. They do not follow mathematics and often mess it up in more ways than I can imagine.
I got immediately attracted to the puzzle Oleg Polubasov recently posted on Facebook.
Puzzle. A rectangular clearing in a forest is an N-by-M grid, and some of the cells contain a tower. There are no towers in the cells that neighbor the forest. A tower protects its own cell completely and parts of the eight neighboring cells at a depth of half of a cell. Here by neighbors, we mean the cells horizontally, vertically, and diagonally adjacent to the given cell. In particular, if each cell is one square unit, a tower protects four square units. The protected area forms a square with borders that lie in between the grid lines. A tsar knows the towers' locations and wants to calculate the protected area. Prove that the following formula gives the answer: the number of 2-by-2 subgrids that contain at least 1 tower.

I like this puzzle because it has an elegant solution. But there is more. The puzzle reminds me of one of my favorite novels by Arkady and Boris Strugatsky: The Inhabited Island, also known as Prisoners of Power. This is a science fiction novel where Max Kammerer, a space explorer, ends up on a planet with desolate people who, twice daily, experience sudden bouts of enthusiasm and allegiance to the government. Later, it becomes clear that the love for the rulers comes from towers that broadcast mind-control signals suppressing critical thinking and making people prone to believe propaganda.
The novel was written in 1969 but accurately describes the modern Russian propaganda machine. It appears that there is no need for a secret signal. Just synchronized propaganda on government-controlled TV turns off people's brains.
A Whitney umbrella is a cool surface I wanted to crochet. The umbrella continues to infinity, and there is no way I want to crochet the whole thing. I wanted to make a finite portion of a Whitney umbrella surrounding the most exciting point.

The result is seen in the picture. Technically, I crocheted not Whitney umbrellas but topologically equivalent surfaces. I am most proud of my secret — and painful — method of crocheting the self-intersecting segment. One day I will spill it.
As Wikipedia defines it: the Whitney umbrella is the union of all straight lines that pass through points of a fixed parabola and are perpendicular to a fixed straight line parallel to the parabola's axis and lies on its perpendicular bisecting plane. If you look at the picture, the fixed straight line is the self-intersection line, which is a continuation of the line segment where the colors are woven through each other. You can find the parabola as the curve formed by the two-colored edge on either side of the umbrella. Oops, I forgot that only three of these umbrellas are made of two colors.
The Whitney umbrella is a ruled surface, meaning that for every point, there is a straight line on the surface that passes through the point. A ruled surface can be visually described as the set of points swept by a moving straight line.
Oh, look, the stitched rows can pretend to be these straight lines. Actually, if I fold these thingies, the stitched rows ARE straight lines. But, when I make the edges into parabolas, the rows stop being straight. In the real Whitney umbrella, if you look along the intersection line, the straight lines are closer to each other than they are along the parabola. But in crochets, the distances between rows have to be fixed. If my crochets are folded, they become rectangles and ruled surfaces. The real Whitney umbrella does not fold into a plane.
The Whitney umbrella is famous for being the only stable singularity of mappings from R2 to R3. I am grateful to Paul Seidel for emailing me the proof. This singularity is so famous it even has two names: pinch point and cuspidal point. Though my crochets are not exactly Whitney umbrellas, they show this singularity. Hooray! I found a secret way to crochet the most famous stable singularity!

My favorite of the Escher plane tessellations is the one with shells. It is stunning, and the mathematics behind it is beautiful. I want to thank the late John Conway for teaching me the secret of this drawing.
Mathematicians are interested in tessellations because of the symmetries behind them. This tessellation has translational and rotational symmetries. Can you find them?
When I ask my students to find the rotational symmetries, they immediately tell me that they see two different 4-fold points, aka points where 90-degree rotations preserve the drawing. One point, I call G, is where four greenish shells meet, and one point, I call R, is where four reddish shells meet.
As you might have guessed, the students' answer is not quite correct. There is more to the picture. Look at a dark-brown shell that looks like a curvy rectangle. This shape has markings. Now look at a specific point R and its four closest brown shells. You can see that going around this point R, the brown shells alternate their orientation: the darker side of these shells either faces towards point R or away.
The big secret of this artwork is that it contains TWO symmetry groups: a group and a subgroup. If we ignore the markings on the brown shells and consider them one solid color, then point R is indeed a 4-fold symmetry point. In addition, the center of the brown shape is a 2-fold symmetry point. Thus, the symmetry group of this simplified drawing is 442 in orbifold notation.
If we take the markings of the brown shells into account, then point R is not a 4-fold rotation, it is a 2-fold rotation. Point G keeps the property of being a 4-fold rotation. If you know your symmetry groups, you can conclude that there should be another 4-fold rotation. But where is it?
I will spill my answer. The symmetry point G is not ONE symmetry point anymore. There are two different points where greenish shells meet. The dark side of the brown shells faces one of them and looks away from the other.
The dark secret of this drawing is that it demonstrates two symmetry groups: group 442 and its subgroup 442, with different fundamental regions. To see the secret, you must look closely at a dark brown shell and find its darker side.
Here is one of my all-time favorite problems.
Puzzle. Four glasses are placed on the four corners of a square rotating table; each glass is either right-side up or upside down. You need to turn them all in the same direction, either all facing up or all down. You may do so by grasping any two glasses and turning either none, one of them, or both over.
There are two catches: 1) You are blindfolded, and 2) the table is spun after each round. Assuming a bell rings when you have them all facing the same way, how do you do it?
When I first heard this problem, the person who tortured me with it forgot to mention the bell. The problem was impossible: there was no feedback. Then, the bell was mentioned. It was an aha moment: you get information, but only a confirmation that the problem is solved. I tried to think about the puzzle backwards. What could be my last step? Assume that I know that the glasses alternate around the table: up, down, up, down. Then, as my last step, I can reach for the diagonal glasses and turn them over.
This is how you might start thinking about this puzzle. You can find the rest of the solution on the puzzle's Wikipedia page.
Here is a wonderful variation, proposed by Michael Hotiner from Ukraine, that appeared ten years ago at a puzzle competition. This variation is not cheap; the players must pay with their lives, albeit virtual ones.
Puzzle setup. Consider a computer game where at level M, there is an M-sided rotating table with glasses at each corner. The setup is similar to the four-glasses puzzle above. The player is blindfolded, and the table rotates between rounds. As soon as level M is over, if all the glasses face one direction, the bell rings, and the player moves to the next level, M+1.
At each round, the player can decide on the number N of glasses to touch. Upon deciding, they have to pay N! lives for that round. Then, the player can touch the glasses one by one, choosing the next glass depending on how the previous glasses are oriented. After all the glasses are touched, the player can decide which ones to turn upside down.
Let's see what happens at the very beginning of this game. The game starts at level 1, with only one glass. The round is solved before it starts. The cost is 0. The bell rings, and the game immediately goes to level 2.
Consider level 2. If the bell doesn't ring immediately, the glasses face different directions. The cheapest way to proceed is to choose N = 1 and turn any glass. The cost is 1.
Consider level 3. A player can solve it in one round by touching all three glasses and turning them the same way. The cost is 3! = 6. There is a cheaper method that costs 4 lives in two rounds. In the first round, the player can touch any two glasses and turn both of them up. If the bell doesn't ring, then the third glass is upside down. In the next round, the player can touch two glasses. If one is upside down, that glass should be turned up. If both glasses are right side up, then the player should turn both of them over to finish the round.
Puzzle tasks.
- Find a way to pass level 3 using only three lives.
- Find the cheapest way to pass level 4.
- Find the cheapest way for level 6.
- Find a way to pass level 5 using only 30 lives.
"Do you really hope to get hired here? We will never hire a woman physicist." This was my friend's job interview here in the US, though many years ago.
Another friend had an adviser who insisted that to recommend her for a PhD he needed to get into her pant first.
I heard more stories over the years, but my personal experience with gender bias was not so dramatic. Or, it could be that I didn't pay attention. Let me start with my most memorable story.
Why did I get an NSF postdoc? Thirty years ago, I had recently arrived in the US, and just had a baby. A friend suggested that I apply for an NSF postdoc. I applied, and I got it. I was elated, but my happiness didn't last long. It lasted until some bitter guy, who didn't get into a postdoc, told me I got the position only because I was a woman. This was the first time I heard that gender might play a role in such decisions. I was devastated. To this day, I still do not know whether it was my talents or my gender that got me the postdoc. For many years after, I had impostor syndrome.
I wrote a blog essay, Polite Gender Bias, about some of my other stories. Each individual case might not seem gender-related, but they were repeated too many times, so I became sensitive. I call these stories:
Here is a more recent story. I do not know whether I should be proud, angry, or embarrassed.
Where is the sugar? From time to time, in the MIT math department tea room, I am asked where is the sugar, or some similar things. This often happens when there are several males in the room. Why was I chosen? It could be that I look friendly and have a great smile, and this is why people approach me. Or people might assume that, being a woman, I am a secretary who knows everything about the kitchen. Or, they might assume that, being overweight, I love sugar and know about every secret sugar stash in any kitchen.
Here is a story where I know exactly how I felt: I was angry.
Can I say a word? I was invited to a lunch discussion on gender issues at our MIT math department. I am not faculty, so I was sure the only reason I was there was because they wanted more female participants. People around me enthusiastically praised our department's handling of gender issues. I tried to speak many times, but some guy would always interrupt me. I was about to start laughing very loudly at the irony of the situation when our department head finally noticed what was going on and gave me a chance to say a word. The situation was resolved then, but I regret that I didn't start laughing.
As stories pile up, I become more vocal. I am tired of being nice at my own expense. Now people think I am a bitch. So be it.
Putin's bodyguards `collect his excrement on trips abroad and take it back to Russia with them'. This was an article in the Independent. Presumably, Putin is afraid that someone can analyze his waste to get information about his health. Here is a quote from the article.
According to the report, members of the Russian president's Federal Protection Service (FPS) are responsible for collecting his bodily waste in specialised packets which are then placed in a dedicated briefcase for the journey home.
Here is my joke on the subject.
Joke. Putin's guard collecting his waste wrote a book of memoirs. The book has two chapters: Number One and Number Two.
One of my all-time favorite puzzles is about tiling a chessboard with 1-by-2 dominoes. But the chessboard is special: two cells at the opposite corners are removed. A similar elegant chessboard puzzle recently appeared on Facebook.
Puzzle. Our special chessboard has one corner cell removed. On each of the remaining cells, there is an ant. At a signal, each ant moves two cells horizontally or vertically (for example, an ant can move from b3 to b5). Is it possible that after all the ants perform their move, each of the 63 cells will have an ant?
This puzzle is a variation of another puzzle, where all the setup is the same, but each ant moves only one cell horizontally or vertically. You can start with this variation, as it is easier.
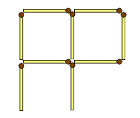
This puzzle was in a homework assignment I gave to my students.
Puzzle. In the given configuration of matches, move two matches to form three squares.
I assume that the intended solution is the one below. Its appeal is that it has three squares of the same size and no dangling matches.

As usual, my students were inventive and suggested many alternative solutions.
I recently stumbled upon the following challenge on Facebook.
Puzzle. Type the number of seconds in a week using the smallest number of characters.
I lied. The challenge was to type the same number using the smallest number of clicks on a computer keyboard. There is a slight difference, and I like my version better.
The Wythoff array is an array of integers that can be defined through Wythoff's game. For my purposes, I will skip over Wythoff's game and define his array using Fibonacci numbers.
You probably heard about binary, ternary, decanary, and other bases. I am sure you know the decanary base: it is our standard decimal system. But, have you ever heard about the Fibonacci base?
Let me define it. Any positive integer can be represented uniquely as a sum of distinct Fibonacci numbers that are not neighbors. For example, 16 is 13 + 3. Now, we just write ones for Fibonacci numbers that we used and zeros for unused Fibonacci numbers, so that the digit corresponding to Fibonacci number 1 is last. (The digit corresponding to Fibonacci number 2 is second to last). Thus, 16 in the Fibonacci base is 100100. The result looks like binary, but it will never have two consecutive ones. Such a representation is called the Zeckendorf representation.
What happens if we add 0 at the end of a number in its Zeckendorf representation? This is like multiplying by 2 in binary. But, in the Fibonacci base, it corresponds to replacing every Fibonacci number in the sum with the next Fibonacci number. The result is called the Fibonacci successor. For example, the Fibonacci successor of 16 has the Zeckendorf representation 1001000 and is equal to 21 + 5 = 26.
Now back to the Wythoff array. The first row consists of the Fibonacci numbers in order. Their Zeckendorf representations look like powers of two in binary. The first column consists of numbers ending in 1 in the Zeckendorf representation, in increasing order. In other words, the Zeckendorf representations of numbers in the first column resemble odd numbers in binary. To finish the definition of the array, each number in the nth column is the Fibonacci successor of a number to its left.
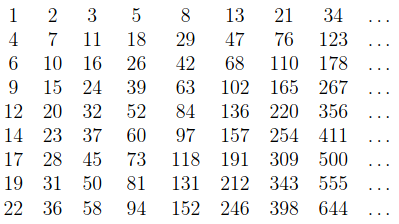
As an example, let's calculate the first three numbers of the second row. The smallest number that is not a Fibonacci number and looks odd in its Zeckendorf representation is 4, represented as 101 (remember, we are not allowed to have two consecutive ones). We place 4 in the first column of the second row. The next number in the second row has to be the Fibonacci successor of 4, so its Zeckendorf representation has to be 1010. This number equals 5+2 = 7. The Fibonacci successor of 7 is 11, with Zeckendorf representation 10100.
John Conway and Alex Ryba wrote a paper where they studied the Wythoff array. They continued the array to the left and drew walls according to a few rules. Here is a picture of their result. The picture is too small to make out the numbers, but you can see the shape, which looks like the Empire State Building. Oops, I forgot to mention, the paper is called The Extra Fibonacci Series and the Empire State Building.

My last year's PRIMES STEP senior group (Eric Chen, Adam Ge, Andrew Kalashnikov, Ella Kim, Evin Liang, Mira Lubashev, Matthew Qian, Rohith Raghavan, Benjamin Taycher, and Samuel Wang) studied the Conway-Ryba paper and decided to generalize it to Tribonacci numbers.
Just a reminder. The Tribonacci sequence starts as 0, 0, 1, 1, 2, 4, 7, 13, 24, 44, and continues so that any next term is the sum of the three previous terms. For example, the next term after 44 is 81.
Now we need an analog of the Wythoff array for Tribonacci numbers. My readers might by now guess why I chose the above definition of the Wythoff array. Yes, this definition is perfect for generalizing to Tribonacci numbers.
We start by defining the Tribonacci base. We can represent every integer uniquely as a sum of distinct Tribonacci numbers on the condition that there are no three consecutive Tribonacci numbers in the sum. This is called a Tribonacci representation. We can express it with zeros and ones, and there will never be three ones in a row. For example, 16 can be expressed as a sum of Tribonacci numbers in the following way: 16 = 13 + 2 + 1. Thus, its Tribonacci representation is 10011.
We can define a Tribonacci successor, similarly to the Fibonacci successor, by adding a zero in the Tribonacci representation. For example, the Tribonacci successor of 16 has to have the Tribonacci representation 100110 and is equal to 24 + 4 + 2 = 30.
Now, we define the Tribonacci array similarly to the Wythoff array. The first row of the Tribonacci array consists of distinct Tribonacci numbers in order. The first column consists of integers whose Tribonacci representations end in 1. The number in the nth column is a Tribonacci successor of the number to its left.
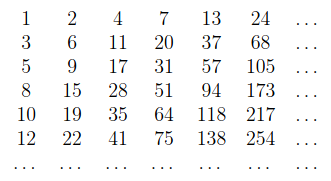
We found many cool properties of the Tribonacci array. They are in our paper, Generalizing the Wythoff Array and other Fibonacci Facts to Tribonacci Numbers, posted on the arXiv. Let me give you three examples of these awesome properties.
It is easy to extend the Tribonacci array to the left, but this extension doesn't have the same nice properties as the extension of the Wythoff array. So finding an Empire State Building, or any other building, in the Tribonacci array is futile.

I agreed to review the book, The Raven's Hat, because of the hats. I love hat puzzles. When I give them to my students, I bring hats to class to reenact the solutions.
The book contains eight awesome puzzles as well as ideas for playing with them. I both loved and hated this book. I loved it because it is great, and hated it because it isn't perfect. Let me start with three places I didn't like.
Consider a famous hat puzzle when there are hats of N colors. The sages are in a line, and hats are put on their heads. As usual, they are not allowed to give each other signals. Each of them has to announce their hat's color, and they want to minimize the number of mistakes.
The big idea is to number the colors. The book suggests that the last sage in line calculates the total number of colors they see modulo N and announces the result to the rest. Then the others, starting from the end of the line, one by one, can calculate and name their hat colors. With this strategy, only the last sage in line might be mistaken.
This is a correct solution, but this is the first place I didn't like. I prefer a different strategy, where everyone assumes that the total sum of the hat colors is 0 modulo N. In this case, every sage makes the same calculation: each sage sums up everything they see or hear and subtract the result from 0 modulo N. This solution is more elegant, since all the sages follow the same rule.
Then the book extends the same puzzle to an infinite number of sages. My second point of contention is that the authors think that, in this case, two sages might be mistaken. No. The answer is still the same, there is a strategy where not more than one sage is mistaken. See my blog post for the solution.
My third pet peeve happened when the authors introduced ballroom dancing in the puzzle on picture hanging. What is the connection between picture hanging and ballroom dancing? I'll keep the book's secret. My beef is with how the roles in ballroom dancing are described. Ballroom dancing is usually danced in pairs with asymmetric roles, which, in the past, were designated for males and females. Gender doesn't play such a big role anymore; anyone can dance any role.
The authors are afraid to be politically incorrect by calling the dancers male and female. Instead, they say that the dancers dance male and female parts. Though formally, this choice of words might be politically correct, it still sounds awkward and draws attention to gender. If the authors ever talked to any person who has ever danced, they would have known that there is a much simpler way to describe dance roles. The dancers are divided into leaders and followers.
Did I ever tell you that reviewing my students' writing is part of my job? So I am good at it and like critiquing other people's writing. Now that my complaints are out, the issues with the book are actually minor.
The book is great. I even bought a second inflatable globe because of this book. The game, described in the book, is to rotate two globes randomly and then find a point on the globes in the same relative position towards the center. The game helped me teach my students that any movement of a sphere is a rotation.
My main goal in this post is to describe the only puzzle in the book that I haven't seen before.
Puzzle. In a group of opera singers, there are two stars who are either friends or enemies. Surprisingly, only the host, who is not an opera singer, knows who the stars are and the nature of their relationship (the stars do not know that they are stars and whether or not they are friends). The group's common goal is to identify the stars and to determine whether they are friends or enemies. To do so, they send a few of the singers to sing opera on a stage, which is divided into two halves: left and right. During the opera, the singers do not move between the halves. After the opera is over, the host classifies the opera. If there were no stars or only one star on stage, he classifies it as "neutral". If both stars were on stage, the opera is a big success or a disaster. If both stars are friends and sing on the same half of the stage, or if they are enemies and sing on different halves, then the opera is a big success. Otherwise, it is a disaster.
What is the best strategy for a group of five singers to determine who are the stars and what is their relationship? What is the smallest number of operas they have to sing to guarantee that they can figure everything out?
It is weird that two people do not know whether they are friends. But sacrifices are needed for mathematics. I am excited that there is a nontrivial puzzle related to information theory, and it is ternary based. All other such puzzles I know are about weighing coins on a balance scale. I wrote too many papers about coin weighing. Now I can switch to opera singers with passionate relationships, secret from themselves.
I stumbled on this puzzle on Facebook the day of the World Cup finals. How timely!
Puzzle. Sixteen teams play a single-elimination tournament, where the losing team is immediately out. The teams have different rankings, and a higher-ranking team always wins against a lower-ranking team. The initial seeding is random.
In the semifinals, A won against B, and C won against D. Given that B is stronger than D, what is the probability that A will become the champion?
Consider a group of people in which some are friends. We assume that friendship is symmetric: if Alice is Bob's friend, then Bob is Alice's friend. That means we can build a friendship graph where vertices are people and edges correspond to friendships. Let's assume that every person has at least one friend, so the friendship graph doesn't have isolated vertices.
Darla needs to conduct research by surveying random pairs of friends. But first, she has to find those pairs. To ensure that the pairs are randomly selected, she must pick two random people from the group, contact them, and ask them whether or not they are friends. If they are, she gives them her questionnaire. If not, Darla wasted tons of time and had to keep looking.
The group she is surveying is enormous. So, when she picks two random people, they typically have never even heard of each other. Bother!
Darla decides to speed up the process. She would pick a random person, ask them for a list of friends, and then randomly pick one person from the list. Since every person has at least one friend, Darla always ends up with a filled questionnaire.
Puzzle question. Why is Darla's method wrong? Can you describe the pairs of friends her method favors?
As my readers know, I run a PRIMES STEP program, where we conduct mathematical research with students in grades 6 through 9. Last year, our junior group wrote the paper, The Struggles of Chessland, which is now posted on the arXiv.
This is the funniest paper ever written at PRIMES STEP. In the paper, the King, with his self-centered Queen and their minions, try to protect their lands in the Bermuda triangle, called the Chessland, which consists of square islands of different sizes.
In the first part of their fairy tale, the King, his lazy Queen, and other chess pieces are trying to survey their islands. The first volunteer for this surveying job is the Knight. The Knight starts somewhere on an island and walks around it by using the knight's moves in chess. The goal is to see every cell, and a Knight can see all cells that are a knight's move away from where he is standing. In other words, every cell is either visited by the Knight or is one knight's move away from a visited cell. In mathematical terms, the Knight walks a path that is a domination set on a knight's graph.
The students found a lot of such paths. The picture shows a surveying path for the Knight for the island of size 7. The students called this pattern a shoelace pattern. They used similar shoelaces to survey any island of size 7 or larger. However, when I look at the picture, I see a cat.
Other chess pieces survey the land too. Funnily, the King surveys better when he is drunk. Do you know why? Take a look at the paper.
After all the islands had been surveyed, enemy spies started to appear in Chessland, and our band of chess pieces tried to trap them. My students invented the rules for trapping enemies. An example of the black Queen being trapped is in the picture below, and the rules are the following. Wherever the black Queen might move, should be under attack by a white queen. Also, white queens can't directly attack the black Queen, or each other.
Oh! I forgot to mention: the trapping should use as few white queens as possible. Also, if the enemy is not a queen but another kind of chess piece, it can only be trapped by its own kind.
The trapping can be described in terms of graph theory. The black Queen is located at a vertex of the queen's graph. The white queens should be positioned at vertices in such a way that they are not neighbors of the black Queen or each other. In addition, any vertex that is a neighbor of the black Queen, has to be a neighbor of at least one white queen.
This year's PRIMES STEP project was a real chess adventure!
The 2018 International Collegiate Programming Contest (ICPC) had a very hard problem which is of interest to mathematicians. The problem was proposed by super-coder Derek Kisman. Here is the problem as it was presented at the contest.
Problem J. Uncrossed Knight's Tour. A well-known puzzle is to "tour" all the squares of an 8 × 8 chessboard using a knight, which is a piece that can move only by jumping one square in one direction and two squares in an orthogonal direction. The knight must visit every square of the chessboard, without repeats, and then return to its starting square. There are many ways to do this, and the chessboard size is manageable, so it is a reasonable puzzle for a human to solve.
However, you have access to a computer, and some coding skills! So, we will give you a harder version of this problem on a rectangular m × n chessboard with an additional constraint: the knight may never cross its own path. If you imagine its path consisting of straight line segments connecting the centers of squares it jumps between, these segments must form a simple polygon; that is, no two segments intersect or touch, except that consecutive segments touch at their common end point. This constraint makes it impossible to visit every square, so instead you must maximize the number of squares the knight visits. We keep the constraint that the knight must return to its starting square. Figure J.1 shows an optimal solution for the first sample input, a 6 × 6 board.
The input consists of a single line containing two integers m (1 ≤ m ≤ 8) and n (1 ≤ n ≤ 1015), giving the dimensions of the rectangular chessboard.
Mathematicians know many things about knight tours on a standard 8 × 8 chessboard. But one of the limits in this puzzle is so huge, that the answer to this computational puzzle constitutes a new mathematical discovery. Unsurprisingly, no one solved this puzzle during the contest. A well-written solution summary is available on the ICPC website. The solution requires dynamic programming and a realization that tours have to have repeating patterns.
Since no one solved this problem during the competition, it is useful that, in addition to the solution summary, Derek posted his innovative code online. The two figures below (courtesy of Derek Kisman) show his answer for the longest closed tour on a 6 × 24 board and the longest open tour on a 6 × 26 board.


Derek got interested in uncrossed knight's tours after reading my blog post, 2014 Math Festival in Moscow, where I presented the following problem given at that festival to 7th graders.
Problem. Inside a 5 × 8 rectangle, Bart draws closed paths that follow diagonals of 1 × 2 rectangles. Find the longest possible path.
The 2014 Math Festival organizers offered an extra point for every diagonal on top of 16. It is funny that the organizers obfuscated that it is useless to try and find 17 diagonals, as the number of diagonals has to be even. The official solution, shown below, had 24 diagonals.
In the solution booklet, the organizers mentioned that they did not know the best answer to their own question. They hoped that the longest possible path matched their official solution.
In Derek's notation, the above problem is equivalent to finding the largest uncrossed knight's closed tour on a 6 × 9 grid. And Derek proved that, indeed, 24 is the largest tour. While proving this, he also calculated the answer for gazillions of other boards.
We can go even further: beyond gazillions. Let's consider what happens on m × n boards, where m is fixed, and n is astronomically large. Suppose fm(n) is the largest size of an uncrossed knight's closed tour on the m × n board and gm(n) is the largest size of an uncrossed open tour.
The answer has repeating patterns everywhere except around the ends of the board. We would expect that the number of possible repeating patterns is finite. Moreover, for large boards, only the densest patterns would appear. This means that asymptotically, both functions f and g are linear functions of n. On top of that, as each pattern is periodic, the behavior at the ends of the long boards should become periodic as well. Hence, the difference functions of f and g for fixed m would eventually become periodic. (Here, the f's difference function, which I denote D(fm) is defined as follows: D(fm)(n) = fm(n+1) - fm(n).)
That means we can solve a more difficult problem. We do not need the limits for n. It should be possible to calculate these functions for a given m and any n (even if n is way more than a gazillion). I am being over-optimistic here. First, we need some mathematical theory to find the bounds for where the periodic behavior has to start and estimate the size of the period. Suppose we can prove that for D(f6)(n), the eventual period has to start before n reaches A, and the length of the eventual period is not more than B. Then, we need to calculate the A + 2B values of the function f6(n) to know the function for any n.
Derek actually calculated the functions fm(n) and gm(n) for m up to 9 and n up to infinity. More precisely, he found the cycles I am describing above. What a mindblowing achievement!
My former IMO coach, Gregory Galperin, converted a famous joke into a logic puzzle, adding a variation.
Puzzle. Ten logicians walked into a cafe. Each knew whether they wanted tea or coffee, but no one knew each other's preferences. When they sat at a table, the waiter asked loudly, "Will everyone be having coffee?" Then the waiter went around the table, writing down each person's answer.
There were three possible answers: "I don't know", "Yes", and "No". All answers were truthful and spoken loudly so that all group members heard them.
- Suppose the first nine people said, "I don't know", and the tenth person said, "Yes". How many of them wanted coffee?
- Suppose the sixth and the seventh answers were not the same. How many people said, "I don't know", how many said, "No", and how many said, "Yes". Find the smallest number of people who for sure would have ordered coffee and the smallest number who for sure would have wanted tea?
Here are some problems that I liked from the YuMSh (Youths Math School in St. Petersburg) Olympiad.
Problem for 6th grade. Twenty people from an island of knights and knaves have a party. Knights always tell the truth, and knaves always lie. Each party-goer got a card with a different number from 1 to 20. When they were asked about their numbers, each answered with a number from 1 to 20. The sum of all the answers is 156. What is the minimum possible number of liars that have to be at the party?
Problem for 7th grade. Alice and Bob bought a deck of playing cards (52 cards total) and took turns gluing the cards on the wall one at a time. Alice was first. The game is lost if, after a move, the wall has 4 cards of the same suit or 4 cards of consecutive values (for example, 8-9-10-jack). Can Alice or Bob guarantee themselves a win, regardless of their opponent's moves?
Problem for 7th grade. Buddhist monks gather in an infinite cave where a finite number of prime numbers are written on the wall. The numbers might not be distinct. Every second, one of the monks performs one of the following operations.
Every time they do it, they erase the old number and write the new one. The rule is that the new number has to be greater than the old one. If a composite number gets written on the wall of this cave, then the world collapses into nothingness. Can the monks save the world for eternity?
Problem for 8th grade. The incenter of a triangle is equidistant from the midpoints of the sides of the triangle. Prove that the triangle is equilateral.
Problem for 9th grade. Bob was given 30 distinct natural numbers. He wrote down all the 435 pairwise sums. It appears that among those sums, 230 are divisible by 3. How many of the original 30 numbers are divisible by 3?
I recently posted a cute puzzle about poisoned wine. Today, I would like to discuss this puzzle's variation with N total glasses, of which two are poisoned.
Puzzle. N glasses of wine are placed in a circle on a round table. S sages are invited to take the following challenge. In the presence of the first sage, N − 2 glasses are filled with good wine and the other two with poisoned wine, indistinguishable from the good wine. After drinking the poisoned wine, the person will die a terrible tormented death. Each sage has to drink one full glass. The first sage is not allowed to give any hints to the other sages, but they can see which glass he chooses before making their own selection. The sages can agree on their strategy beforehand. For which S can you find a strategy to keep them all alive?
What does this have to do with rulers, and what are those? I am grateful to Konstantin Knop for showing me a solution with rulers. But first, let's define them.
A sparse ruler is a ruler in which some distance marks may be missing. For example, suppose we have a ruler of length 6, with only one mark at a distance 1 from the left. We can still measure distances 1, 5, and 6. Such a ruler is often described as {0,1,6} to emphasize its marks, endpoints, and size.
A complete sparse ruler is a sparse ruler that allows one to measure any integer distance up to its full length. For example, the ruler {0,1,6} is not complete. It can't measure distances 2, 3, and 4. Thus, if we add the marks at 2, 3, and 4, such a ruler becomes complete.
A complete sparse ruler is called minimal if it uses as few marks as possible. In our previous example, the ruler {0,1,2,3,4,6} is not minimal. The distance between marks 1 and 4 is 3, so if we remove mark 3, we can still measure any distance. We can remove mark 2 too. The ruler {0,1,4,6} with marks 1 and 4 is minimal.
Oops. I forgot that we have a round table. This means we need to look at cyclic rulers: the idea is the same, but the numbers wrap around. For example, consider the cyclic ruler {0,1,4,6} of length 6, where 0 and 6 is the same point. This ruler has three marks at 0, 1, and 4.
Going back to the puzzle, suppose N = 6, aka there are six glasses around the table. The sages need to agree on a complete cyclic ruler, for example, the one described above. As this ruler contains any possible difference between the marks, the first sage can mentally place the ruler on the table so that the marks cover poisoned glasses. He signals the position of the ruler by drinking his glass. The sages can agree that the glass drunk by the first sage corresponds to position −1 on the ruler, and the other sages avoid the first, second, and fifth glass clockwise from the chosen glass.
In this case, three glasses are not covered by the ruler's marks. This means three sages can be saved.
To summarize, the sages need a complete ruler, as such a ruler can always cover two glasses at any distance from each other with its marks. The number of sages that can be saved by such a ruler is N minus the number of marks. To save more sages, we want to find a minimal ruler.
There are actually more cool rulers. A ruler is called maximal if it is the longest complete ruler with a given number of marks. For example, the non-cyclic ruler {0,1,4,6} is maximal. A ruler is optimal if it is both maximal and minimal. Thus, the ruler {0,1,4,6} is also optimal.
There are other types of rulers called Golomb rulers. They require measured distances to be distinct rather than covering all possibilities. Formally, a Golomb ruler is a ruler with a set of marks at integer positions such that no two pairs of marks are the same distance apart. If, however, a Golomb ruler can measure all the distances, it is called a perfect Golomb ruler. As we can deduce, a perfect Golomb ruler is a complete sparse ruler. I leave it to the reader to show that a perfect Golomb ruler must be a minimal complete sparse ruler.
The rulers rule!
I wrote a lot about the inventiveness of my students. Here is more proof.
Puzzle. A police officer saw a truck driver going the wrong way down a one-way street but didn't try to stop him. Why?
Many of my students came up with the expected answer:
The truck driver was walking.
They also found some legit ways for a truck driver to not be stopped.
Some more ideas, rather far-fetched.
Some funny ones.
I often receive letters from parents of math geniuses — "My twelve-year-old is reading an algebraic geometry book: accept him to PRIMES," or "My ten-year-old finished her calculus course: here is her picture to post on your blog," or "My two-year-old knows the multiplication table, can you write a research paper with him?" The last letter was a sarcastic extrapolation.
I am happy to hear that there are a lot of math geniuses out there. They are potentially our future PRIMES and PRIMES STEP students. But, it is difficult to impress me. The fact that children know things early doesn't tell me much. I've seen a student who didn't know arithmetic and managed to pass calculus. I've also met a student claiming the full knowledge of fusion categories, which later appeared to be from half-watching a five-minute YouTube video.
There are a lot of products catering to parents who want to bring up geniuses. My grandson received a calculus book for his first birthday: Introductory Calculus For Infants. Ten years later, he still is not ready for calculus.
Back to gifted children. Once a mom brought us her kid, who I can't forget. The child bragged that he solved 30 thousand math problems. What do you think my first thought was? Actually, I had two first thoughts: 1) Why on Earth would anyone count all the problems they solved? 2) And, what is the difficulty of the problems he solved 30 thousand of?
From time to time, I receive an email from a parent whose child is a true math genius. My answer to this parent is the same as to any other parent: "Let your child apply to our programs. We do a great job at working with math geniuses."
Our programs' admissions are done by entrance tests. Surprisingly, or not surprisingly, the heavily advertised kids often do poorly on these tests. It could be that the parents overestimate their children's abilities. But sometimes, the situation is more interesting and sad: I have seen children who sabotage the entrance tests so as not to be accepted into our programs. We also had students give us hints on their application forms that they were forced to apply.
In the first version of this essay, I wrote funny stories of what these students did. Then, I erased the stories. I do not want the parents to know how their children are trying to free themselves.
Dear parents, do not push your children into our programs. If they do not want to be mathematicians, you are decreasing their chances of getting into a good college. Imagine an admission officer who reads an essay from a student who wants to be a doctor but wastes ten hours a week on a prestigious math research program. Such a student doesn't qualify as a potential math genius, as their passion lies elsewhere. Nor does this student qualify as a future doctor, as they didn't do anything to pursue their claimed passion. In the end, the student is written off as a person with weak character.
On the other hand, the students who do want to be in our programs, thrive. They often start breathing mathematics and are extremely successful. Encourage your children to apply to our programs if they have BOTH: the gift for mathematics and the heart for it.
This puzzle was in last week's homework.
Puzzle. How can an egg fly three meters and not break?
The expected answer:
Some students tried to protect the egg:
Other students specified qualities of an egg making it more resistant:
Here are some more elaborate explanations:
To conclude this essay, here is a punny answer:
I am so tired of spam emails. I keep thinking about how we can fight spam, and here is an idea.
Gmail should change its system: every email you send to me would cost 1 dollar, payable to me. We can add an exception for people on my contact list. Everyone else, pay up!
I do not often contact strangers. But if I do, it is always important. So paying 1 dollar seems more than fair. On the other hand, this system will immediately discourage mass emails to strangers. Spam would go down, and I would stop receiving emails inviting me to buy a pill to increase the size of a body part I do not have.
This idea of getting paid for reading an email is not new. It was implemented by Jim Sanborn, the creator of the famous Kryptos sculpture. Kryptos is located at the CIA headquarters and has four encrypted messages. People tried to decrypt them and would send Jim their wrong solutions. Jim got tired of all the emails and administered Kryptos fees. Anyone who wants Jim to check their solution, can do so by paying him 50 dollars. I wonder if Jim would still charge the fee if someone sent him the correct solution.
Thinking about it, I would like the payable email system to be customizable, so I can charge whatever I want. After all, I do value my time.
Gmail could get a small percentage. Either Gmail, together with me, gets rich, or spam goes away. Both outcomes would make my life easier.
Puzzle. A goat was on a 10-meter leash. Yet it managed to go 300 meters away from the post. How come?
The standard answer. The leash wasn't attached to the post.
My students scrutinized the puzzle and found some other possible ambiguities. For example, there might be two posts: the goat was leashed to one and was far away from the other. In another example, the timing is not given. It is possible that the goat was on the leash at one time and unleashed and far away from the post at another time. Here is my favorite answer.
My favorite answer. The goat ate the leash.
Puzzle. Find the largest and the smallest 4-digit numbers n such that when you erase the first two digits of n, you get the sum of the digits of n.
I recently posted a gnome puzzle by Alexander Gribalko.
Puzzle. Nine gnomes repeat the following procedure three times. They arrange themselves on a 3 by 3 chessboard with one gnome per cell and greet all of their orthogonal neighbors with handshakes. Prove that not all pairs of gnomes greet each other.
As often happens with my blog puzzles, I used this puzzle as homework for my students. They calculated that the total number of handshakes needed for all nine gnomes to greet each other is 36. On the other hand, each arrangement of gnomes creates 12 handshakes. This means that the numbers are tight: no greeting can be wasted, and every pair of gnomes need to greet each other exactly once. The students then studied different cases to prove this was impossible.
In each arrangement, a gnome can have either 2, 3, or 4 handshakes. Hence, we can distribute handshakes over three placements as 2+2+4 or 2+3+3. It follows that if a gnome is ever in the center of the grid, he has to be in a corner for the other two arrangements. Therefore, the three gnomes who end up in the center for one of the arrangements never greet each other.
However, I always love solutions that involve coloring the board in a checkerboard manner. Here is my solution.
Solution. Let's color the board in a checkerboard manner. We assign each gnome a binary string, of length 3, describing the colors of the cells where the gnome was in each placement. There are 8 different possible strings. It follows that at least two gnomes are assigned the same string. But they can't greet each other if they are standing on the same colors in each arrangement!
* * *
I hate getting into debates about Möbius strips. They're always one-sided.
* * *
North Korea's ballistic missile test failed due to a bug in Windows. The next missile containing a bug report has been automatically sent to Microsoft.
* * *
4 out of 3 people have trouble with fractions.
* * *
Do you know what seems odd to me?
Numbers that aren't divisible by two.
* * *
Why was algebra so easy for the Romans?
X was always 10.
My readers know that I love hat puzzles. This is why I decided to turn a number trick by Konstantin Knop (in Russian) into a hat trick.
Hat Trick. The audience has a bottomless supply of hats in ten different colors. They arrange ten people in a line and put one of the hats on each person. Then the magician's assistant comes in and removes a hat from one of the ten people. After that, the magician appears and, abracadabra, guesses the color of the removed hat. The magician and the assistant agreed on a strategy beforehand. What is it?
Keep in mind that this trick won't work with fewer than ten colors. As a bonus, can you explain why?

As my readers know, I am devoted to my students. When I need something I can't buy, I try to make it. That is why I crocheted a lot of mathematical objects. One day, I resolved to have in my possession a Seifert surface bounded by Borromean rings (a two-sided surface that has Borromean rings as its border).
However, my crocheting skills were not advanced enough, so I signed up for a wet and needle felting workshop. When I showed up, Linda, our teacher, revealed her lesson plan: a felted soap with a nice pink heart on top. It looked cool to have soap inside a sponge, not to mention that wool is anti-bacterial. But I had bigger plans than soap and eagerly waited for no one else to show up.
When my dream materialized, and, as I had hoped, no one else was interested in felt, I asked Linda if we could drop the hearty soap and make my dream thingy. She agreed, but my plan didn't survive for long. As soon as Linda saw a picture of what I wanted, she got scared. Seifert surfaces were not in the cards, so soap it was. I told her that there was no way I was going to needle-felt a pink heart onto my felted soap. I ended up with a blue Sierpiński gasket.
We had a great time. Linda was teaching me felting, and I was teaching her math. I am a good teacher, so even felters working on a farm enjoy my lessons.
After the workshop, I went online and found my dream surface on Shapeways. In the end, I was happy to just buy it and not have to make it.

But my felting workshop wasn't a waste of time: tomorrow I will wash myself with a gasket.
A combinatorial games section? At a math competition? I have never heard of it before. But here it is, at the Lomonosov Tournament. The first problem is from the 2012 Tournament (the link is to a Russian version). The problem is by Alexander Shapovalov. I picked it for its elegance and simplicity.
A rectangular band. You have a paper rectangle of size m by n with grid lines, where both m and n are greater than 1. Two players play the following game. The first player cuts the rectangle along any grid line into two rectangles. The next player picks one of the rectangles and cuts it again along a grid line, and so on. The winner is the player who, after their move, can arrange all the rectangles into a band of width 1. Which player is guaranteed a win regardless of the moves of their partner? Consider two cases.
- One of the numbers, m or n, is even;
- Both m and n are odd.
The next problem, by I. Raskin, is from the 2015 Tournament (in Russian). The problem is about fruits, and I know a lot of great puzzles with bananas and oranges, so I immediately got attracted to this one.
The original version had three types of fruit starting with the letters a, b, and c in Russian. They were oranges, bananas, and plums. I reused bananas and replaced oranges with apples, but I got stuck on the letter c. The players in this game eat their fruits, so using cantaloupes seemed like overkill. Plus, I am on a diet, so I decided on cherries.
Fruits. There are a apples, b bananas, and c cherries on the table. Two players play a game where one move consists of eating two different fruits. The person who can't move loses. Assuming the players use their best strategies, would the first or the second player win in the following cases?
- a = 1 (the answer might depend on the values of b and c);
- a = 6, b = 8, c = 10;
- a = 7, b = 9, c = 15;
- a = 19, b = 20, c = 21.
The last problem is from the 2012 Tournament (in Russian). It has great sentimental value for me, as it was created by John Conway. It also reminds me of the famous Frobenius (chicken McNugget) problem.
Coin mintage. Once upon a time, in a faraway kingdom, two treasurers were minting coins. They decided to make it into a game, taking turns minting coins. Each turn, the player chooses a particular integral denomination and mints an infinite supply of coins of this denomination. The rules of the game forbid choosing a new denomination that can be paid with the existing coins. The treasurer who is forced to mint a coin of denomination 1 loses.
- Prove that if the first treasurer starts with denomination 2 or 3, s/he loses.
- Is it profitable for the first treasurer to start with denomination 4?
- Is it profitable for the first treasurer to start with denomination 6?
- Suppose the first treasurer minted coins of denomination 5, and the second treasurer of denomination 6. What is the winning strategy for the first treasurer after that?
- Suppose the first treasurer minted coins of denomination 5, and the second treasurer of denomination k. Prove that the largest denomination available for minting is 4k − 5.
- Prove that the first treasurer can win by starting with denomination 5. (Hint: Suppose the second treasurer replied with denomination k, and the first treasurer minted 4k − 5 after that. If this strategy wins, the problem is solved. However, if after that, the second treasurer wins by minting denomination m, then minting denomination 4k − 5 was the wrong move. What was the right move?)
Here is another exciting puzzle posted on Facebook by Konstantin Knop.
Puzzle. Eight glasses of wine are placed in a circle on a round table. Three sages are invited to take the following challenge. In the presence of the first sage, five glasses are filled with good wine and the other three with poisoned wine, indistinguishable from the good wine. After drinking the poisoned wine, the person will die a terrible tormented death. Each sage has to drink one full glass. The first sage is not allowed to give any hints to the other sages, but they can see which glass he chooses before making their own selection. The three sages can agree on their strategy beforehand. What is the strategy to keep them all alive?
An extra question. Does a strategy exist if fewer than eight glasses are placed around the table?
Let's start with two trivial variations. If there is only one sage, s/he knows which glass to drink. Now, suppose there is only one poisoned glass and any number of sages. If the total number of good glasses is not less than the number of sages, the solution is obvious. The first sage drinks the glass clockwise from the poisoned one, and the other sages continue clockwise.
The next slightly less trivial case involves two sages and two poisoned glasses. If the total number of glasses is at least five, the sages are safe. The reason: there are at least two good glasses in a row. So the sages can agree that the first one drinks a good glass followed clockwise by another good glass. If the total number of glasses is less than 5, there is no reliable strategy, as the reader can check.
The above idea works if the number of sages is S, the number of poisoned glasses is P, and the total number of glasses is T, where T is greater than SP. Then, the strategy is the same since there is a guaranteed continuous stretch of S good glasses.
On the other hand, one can argue that for S and P more than 1, and T = S + P, it is impossible to find a strategy.
Our original problem corresponds to the case S = P = 3, and T = 8. Presumably, the strategy doesn't exist if S = P = 3, and T < 8. If the 8-glasses problem is difficult, here is a much easier version, corresponding to the case S = 2, P = 3, and T = 6.
An Easier Puzzle. Six glasses of wine are placed in a circle on a round table. Two sages are invited to take the following challenge. In the presence of the first sage, three glasses are filled with good wine and the other three with poisoned wine, indistinguishable from the good wine. After drinking the poisoned wine, the person will die a terrible tormented death. Each sage has to drink one full glass. The first sage is not allowed to give any hints to the other sages, but they can see which glass he chooses before making their own selection. The three sages can agree on their strategy beforehand. What is the strategy to keep them all alive?
I am trying to make a point that, mathematically, the Sleeping Beauty problem is resolved, and the Wikipedia article about it should stop assuming that there is an ongoing debate.
The Sleeping Beauty problem. Sleeping Beauty participates in the following experiment. On Sunday, she is put to sleep, and a fair coin is flipped. Regardless of the result of the coin flip, she is awakened on Monday and asked whether she thinks the coin was heads or tails. Regardless of her answer, if the coin was heads, the experiment ends. However, if the coin was tails, she is put back to sleep with her memory erased and awakened again on Tuesday and asked the same question. In this case, the experiment stops on Tuesday. She knows the protocol. She is awakened one morning. From her point of view, what is the probability that the coin was heads?
Here is the solution. If it is Monday, then the probability that the coin is heads is one half. So the probability of Monday/heads is the same as Monday/tails. If the coin is tails, Sleeping Beauty can't distinguish between Monday and Tuesday. So the probability of Monday/tails is the same as Tuesday/tails. Thus, the three cases Monday/heads, Monday/tails, and Tuesday/tails are equally probable. It follows that when she is awakened, the probability of heads is one third.
However, there are still people — called halfers — who think that the probability of heads is one half.
But suppose we ask a different question.
Different question. She is awakened one morning. From her point of view, what is the probability that the day is Tuesday?
As I explained before, when she is awakened, the probability of it being Tuesday is one third. Let us calculate what the halfers think. Suppose they think that the probability of the day being Tuesday is x, then the probability of Monday is 1 − x. Let's calculate the probability of the coin being heads from here. The probability of heads, if today is Tuesday, is zero. The probability of heads, if today is Monday, is 1/2. Therefore, the probability of heads equals 0 · x + (1 − x)/2 = (1 − x)/2. In halfers' view, the resulting calculation equals 1/2. In other words, (1 − x)/2 = 1/2. It follows that x is zero. Doesn't make much sense that the probability of the day being Tuesday is zero, does it?
Halfers are wrong. Wikipedia should update the article.
The Sleeping Beauty problem. Sleeping Beauty participates in the following experiment. On Sunday, she is put to sleep, and a fair coin is flipped. Regardless of the result of the coin flip, she is awakened on Monday and asked whether she thinks the coin was heads or tails. Regardless of her answer, if the coin was heads, the experiment ends. However, if the coin was tails, she is put back to sleep with her memory erased and awakened again on Tuesday and asked the same question. In this case, the experiment stops on Tuesday. She knows the protocol. She is awakened one morning. From her point of view, what is the probability that the coin was heads?
This problem is considered controversial. Some people, called halfers, think that when she is awakened, the probability that the coin was heads is one half. Other people, called thirders, think that when she is awakened, the probability that the coin was heads is one third.
I am a thirder, so let me explain my thinking. If it is Monday, then the probability that the coin is heads is one half. So the probability of Monday/heads is the same as Monday/tails. If the coin is tails, Sleeping Beauty can't distinguish between Monday and Tuesday. So the probability of Monday/tails is the same as Tuesday/tails. Thus, the three cases Monday/heads, Monday/tails, and Tuesday/tails are equally probable, and the answer follows.
This problem is similar to the Monty Hall problem in some ways. The main difference is that The Monty Hall problem stopped being controversial, while Sleeping Beauty problem continues to be. The best argument that helped intuition and led to the resolution of the Monty Hall problem was increasing the number of doors. Similarly, for the Sleeping Beauty problem, we can increase the number of days she is put back to sleep when the coin is tails. Forgive me for the cruelty of this theoretical experiment.
The Sleeping Beauty Variation. Sleeping Beauty participates in the following experiment. On Sunday, she is put to sleep, and a fair coin is flipped. Regardless of the result of the coin flip, she is awakened on Monday and asked whether she thinks the coin was heads or tails. Regardless of her answer, if the coin was heads, the experiment ends. However, if the coin was tails, the experiment continues for 99 more days. Each day, she is put back to sleep with her memory erased and awakened the next day and asked the same question. She knows the protocol. She is awakened one morning. From her point of view, what is the probability that the coin was heads?
In this variation, when she is awakened, she should be almost sure that the coin was tails. I hope it will help halfers feel that, in this case, the probability of heads can't be one half. For me, the argument is the same as before, making the probability that the coin was heads is 1 over 101.
After I wrote this essay, I discovered that Nick Bostrom made the same argument. Though, for tails, he put Sleeping Beauty to sleep one million and one times, which is about 2,740 years. He increased my one hundred days by several orders of magnitude, amplifying our point. Surely, when Sleeping Beauty awakens, she should be almost certain that the coin was tails. After Sleeping Beauty agrees to so much torture, why is the problem still controversial?
We already blogged about the Sleeping beauty problem three times: The Sleeping Beauty Problem, Sleeping Beauty Meets Monty Hall, and Sleeping Beauty and Mondays. The posts were more than ten years ago, but the mathematical community seems to continue being stuck on this problem. So we come back to it.
Problem. Sleeping Beauty participates in the following experiment. On Sunday, she is put to sleep, and a fair coin is flipped. Regardless of the result of the coin flip, she is awakened on Monday and asked whether she thinks the coin was heads or not. If the coin was tails, however, she is put back to sleep with her memory erased, awakened on Tuesday and asked the same question again. She knows the protocol. She is awakened one morning: What is her probability that the coin was heads?
Let's raise the stakes a little bit. Suppose a prize of $1K is set aside for her correct guess of a flip. What should be her strategy?
The problem is ambiguous. We didn't tell you how the prizes are awarded. We see several reasonable scenarios:
Because of selective amnesia, she can't distinguish between her awakenings, thus her strategy has to be the same at every awakening. That is, she should say heads with probability p. The exact number depends on the scenario:
We see that though she is asked to guess the outcome of the coin flip and is rewarded for guessing correctly, her strategy is not to try to maximize the probability of guessing correctly each time. The strategy depends on the reward protocol.
We see that in the first and the sixth scenario, she gets one guess per coin flip. Not surprisingly, it doesn't matter what she chooses to do. The classic Sleeping Beauty problem corresponds to the third scenario. If she wants to improve her chances per guess, she should favor tails.
Let's look at the following variation.
Problem. Suppose Sleeping Beauty's goal is to guess right once, but if she guesses right on Monday, she wins and is not put back to sleep. If she guesses wrong on Monday and the coin was tails, she is put back to sleep with he memory erased. That is, she is given a second chance. What's the right strategy in this case?
As her memory is erased, the only strategy is to do the same thing each time she is awakened. That is to guess heads with probability p. Thus, she guesses correctly at least once with probability p/2 + (1–p)/2 + p(1–p)/2. We see that whatever strategy she chooses, she guesses with probability one half on Monday. She gets an additional chance of p(1–p)/2 to get a correct guess on Tuesday. Her worst strategy is to always guess tails or heads. Her best strategy is to flip a fair coin each time. This way, she has an additional probability of 1/8 to win on Tuesday.
Here is a question to our readers, for the best strategy above, what is her probability on waking that the coin is actually heads? Here is the problem more formally.
Problem. Sleeping Beauty participates in the following experiment. On Sunday, she is put to sleep, and a fair coin is flipped. Regardless of the result of the coin flip, she is awakened on Monday and asked whether she thought the coin was heads or not. Sleeping Beauty answers by flipping a fair coin. If she guesses correctly, or if the Sunday coin was heads, the experiment ends. If the Sunday coin was tails and different from her guess, she is put back to sleep with her memory erased, awakened on Tuesday, and asked the same question again. She knows the protocol. She is awakened one morning: What is her probability that the Sunday coin was heads?

I love Toblerone, but I never paid attention to its logo.
This Swiss chocolate was created in Bern (Berne) more than a hundred years ago. A legend says that Berne's founder loved hunting and vowed to name the city after the first animal he met on his hunt. The animal happened to be a bear, and so the town was named Berne. The bear became a big deal for the town; you even can find the bear on the town's flag and coat of arms.
Theodor Tobler, the creator of Toblerone, put the famous local mountain, Matterhorn, in the logo of Toblerone and hid a bear in the image. He obviously loved his country and town.
Tobler was clearly a wordsmith and invented a fascinating name for his chocolate. As Wikipedia explains, the name Toblerone is a portmanteau combining Tobler's name with the Italian word torrone, which is a type of nougat used in his chocolate. However, Wikipedia doesn't explain that the word Toblerone also contains a secret: the word BERNE (bear).
After writing this, I couldn't resist and bought some dark Toblerone chocolate. Now it brings me pleasure in more ways than one.
There are many cute math problems that use the trivial fact announced in the title. For example, I recently posted the following problem from the 43rd Tournament of Towns.
Problem. Find the largest number n such that for any prime number p greater than 2 and less than n, the difference n − p is also a prime number.
Solution. Prime numbers 3, 5, and 7 have different remainders modulo 3. Thus, for any n, one of the numbers n − 3, n − 5, or n − 7 is divisible by 3. If n > 10, that number that is divisible by 3 is also greater than 3, thus, making it composite. Therefore, the answer to this problem is not greater than 10. Number 10 works, thus, the answer is 10.
Here is another problem using the fact that 3, 5, and 7 have different remainders when divided by 3.
Problem. Find the maximum integer n, such that for any prime p, where p < n, the number n + 2p is prime.

Here is the current picture of my coauthor, Joel Lewis. I remember him from many years ago when he was a graduate student at MIT. I am glad he kept his big smile.
Back to the subject matter. Joel Lewis made a comment on my recent post, thinking-outside-the-box ideas. He mentioned his two theorems:
The Big Point Theorem. Any three lines intersect at a point, provided that the point is big enough.
The Thick Line Theorem. Any three points lie on the same line, provided that the line is thick enough.
I grew up a purist. Mathematics was about mathematics, not about gender. I personally would never have competed in a math competition exclusively for girls. I would have felt diminished somehow. Furthermore, suppose there were separate math competitions for boys, where girls were not allowed. I would have felt outraged. By symmetry, I should have been outraged by math competitions exclusively for girls.
When I first heard about math competitions for girls, I was uncomfortable. I also noticed that my Eastern European friends shared my feelings, while my other friends did not.
There was a stage in my life when I lived in Princeton for seven years and became friends with Ingrid Daubechies, who is NOT Eastern European. She didn't share my extreme views, and we argued a lot. Every spring, there was a big conference for Women-in-Mathematics at the Institute for Advanced Study in Princeton. But I was stubborn and completely ignored it. With one exception: when Ingrid gave a lecture there, I went just to hear her talk.
In 2008, I was living in Boston, worrying about money, as I had just resigned from my industry work to return to mathematics. Out of the blue, Ingrid called to offer me a job at that very same Women-in-Mathematics conference. I admire Ingrid and got excited about working with her. More importantly, I needed the money. So I decided to put aside my prejudice and take the job.
Being part of the conference was a revelation. Although most of the two-week conference was spent on mathematics, there were some women-and-math seminars. There, women discussed bullying by advisers and colleagues, impostor syndrome, workplace bias, the two-body problem, and other issues. And guess what? I went through all of that too. I just never realized it and never talked about it.
My biggest regret was that I hadn't attended the conference earlier. Plus, the conference didn't feel unfair towards men: all lectures and math seminars were open to the public, and some courageous guys sat in.
What about my symmetry test? What happens if we swap genders? Should there be separate math conferences for men, open to the public? The idea makes me laugh. Women are in the minority in math, and many conferences already feel like conferences for men open to the public. My symmetry test doesn't quite work.
But, while I saw how helpful the support was for female mathematicians and for me, something still bugs me. Where is the fine line between minority support and unfairness? Let's look at math clubs for girls. On the surface, there are so many math clubs, so why not have the occasional math club for girls? I can imagine a girl, not me, who would prefer to attend such a club. However, girls' clubs often have sponsors and are much cheaper to attend than regular clubs. This is unfair to boys whose parents can't afford a regular club. It also becomes counterproductive for girls. What if some girls go to such a club, not because they need a special environment but because it is a cheaper club? They are missing out on the fun of learning math together with boys. (Trust me, I know!) So, I am not sure where that line is.
I am older and wiser now. I do not run away from events organized for women in math. I think lunches and dinners for women in math are great. They help female mathematicians find mentors, build networks, and stay in mathematics.
What about my original question: Should there be separate math competitions for girls? In a truly equal society, math competitions should be for everyone. And, though I do not actively oppose girls' competitions anymore, I hope the need for them will die out in my lifetime.
Recently, I stumbled upon three lovely logic puzzles, while scrolling Facebook for news from the Russia-Ukraine war. I will start with an easy puzzle.
Puzzle. A traveler got to an island, where each resident either always tells the truth or always lies. A hundred islanders stood in a circle facing the center, and each told the traveler whether their neighbor to the right was a truth-teller. Based on these statements, the traveler was able to clearly determine how many times he had been lied to. Can you do the same?
In the next puzzle, there is another island where people are either truth-tellers or normal. There are three questions that increase in difficulty.
Puzzle. You are on an island with 65 inhabitants. You know that 63 inhabitants are truth-tellers who always tell the truth, and the other 2 are normal, who can either lie or tell the truth. You are allowed one type of question, "Are all the people on this list truth-tellers?" This question requires a list, which you can create yourself. Moreover, you can have as many different lists as you want. You can pose this question to any islander any number of times. Your goal is to find the two normal people. The easy task is to do it in 30 questions. The medium task is to do it in 14 questions. The hard task is to figure out whether it is possible to do it in fewer than 14 questions.
Here is the last puzzle.
Puzzle. You got to an island with 999 inhabitants. The island's governor tells you, "Each of us is either a truth-teller who always tells the truth, or a liar who always lies. " You go around the island asking each person the same question, "How many liars are on the island?" You get the following replies.
First person, the governor: "There is at least one liar on the island."
The second person: "There are at least two liars on the island."
This continues progressively until the 999th person says: "There are at least 999 liars on the island."
What can you tell about the number of liars and truth-tellers on this island?
I recently wrote an essay, Thinking Inside and Outside the Box, which starts with a famous nine-dots puzzle that kicked off the expression: thinking outside the box. Here is another puzzle with the same nine-dots setup.
Puzzle. What is the smallest number of squares needed to ensure that each dot is in its own region?
Usually, people who try to solve this puzzle come up with the following four-squares solution.
As with the classic nine-dots puzzle, they imagine that the dots are on a grid and try to build squares with sides parallel to the grid lines. What would be the outside-the-box idea? The sides of the squares would not need to be parallel to the grid. This way, we can solve the puzzle with three squares.
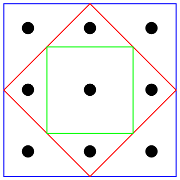
One of my MathRoots students offered a different and awesome solution also using three squares.
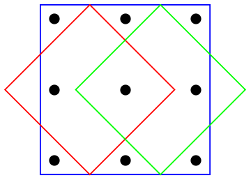
Problem. Find the largest number n such that for any prime number p greater than 2 and less than n, the difference n − p is also a prime number.
The most famous thinking-outside-the-box puzzle is the Nine-Dots puzzle. This puzzle probably started the expression, "To think outside the box". Here is the puzzle.
Puzzle. Without lifting the pencil off the paper, connect the nine dots by drawing four straight continuous lines that pass through all the dots.
Most people attempt something similar to the picture below and fail to connect all the dots.
They try to connect the dots with line segments that fit inside the square box around the dots, mentally restricting themselves to solutions that are literally inside the box.
To get to the correct solution, the line segments should be drawn outside this imaginary box.
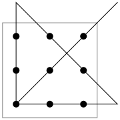
Do you think that four line segments is the best you can do? Jason Rosenhouse showed me a solution for this puzzle that requires only three lines. Here, the outside-the-box idea is to use the thickness of the dots.
This and many other examples of thinking outside the box are included in my paper aptly titled Thinking Inside and Outside the Box and published in the G4G12 Exchange book.
A section of this paper is devoted to my students, who sometimes give unexpected and inventive solutions to famous puzzles. Here is an example of such a puzzle and such solutions that aren't in the paper because I collected them after the paper was published.
Puzzle. Three men were in a boat. It capsized, but only two got their hair wet. Why?
The standard answer is the following: One man was bald.
Lucky for me, my creative students suggested tons of other solutions. For example,
My favorite example, however, is the following.
I still get comments that my place is in the kitchen, and women shouldn't do math. Luckily, occurrences of such events are getting rarer. So the world is progressing in the right direction. But gender bias still exists. Multiple studies show that among people of the same level of intelligence, men are perceived as smarter. In layman's terms, people think women are stupider than they are. I will give my own examples at another time. But now, I want to discuss my model for gender bias.
Let's denote the mathematical strength of a researcher by S. In real life, if the researcher is female, people perceive her strength as smaller than S. Let us assume that there exists a bias coefficient B, a number between 0 and 1 so that a female researcher of strength S is perceived on average as having strength BS. When B is 1, then there is no bias. But the world is not there yet.
In recent years, there has been a push to hire female mathematicians. Suppose a math department has a cutoff C for hiring a math professor. Being eager to hire a female professor, the department slightly reduces the cutoff by the bias reduction coefficient R, where R is a number between 0 and 1. Thus, the cutoff to hire a female professor becomes RC, which is less than C.
Now consider Alice, who has mathematical strength S, such that S ≥ C ≥ BS ≥ RC. She is perfectly qualified to be hired by the department independent of her gender. However, the department members, on average, perceive her strength as not good enough for a male hire but good enough for a female one. Alice is hired. What happens as a result?
Many male colleagues are angry. They think that because of Alice, they couldn't hire a male candidate they believe to be stronger. They also expect Alice to be grateful for the opportunity. How will Alice react? It depends on whether Alice herself is biased. I will give two potential scenarios.
Scenario 1. Alice is biased and realizes she is only hired because she is female. Alice thinks that her strength is below the cutoff C. Alice develops impostor syndrome and doesn't contribute to the department and mathematics as much as she could have, reinforcing everyone's belief that she is weaker than she actually is.
Scenario 2. Alice is not biased but realizes that she was hired for her gender and not for her mathematics. She gets angry too because she knows she is perfectly qualified. She also realizes that the department expects her to be grateful, while another male hire is thanked for taking a similar position. In this scenario, everyone is angry.
In both scenarios, the intent is to fight the bias. But as a result, no one is truly happy. A supportive environment is not created. And the idea that male and female mathematicians differ in strength is reinforced.
Recently, I talked to a male colleague about gender bias. He was adamant that he isn't biased and, as proof, described his contribution to hiring females in his department. This is not proof of being unbiased. This is proof of trying to resolve the bias, either sincerely or due to outside pressure. However, the real proof would be to change one's attitude towards female colleagues. As a female colleague myself, I would notice this change in attitude. But while nothing changes, I can't accept the fact of female hires as proof of no bias.
To truly resolve the bias, we need B to be equal to 1. To improve the situation, people should collectively work on increasing the bias coefficient B. This is more about changing the attitude.
I am for hiring more female mathematicians as professors. But sometimes, I feel like hiring more female mathematicians without addressing the attitude is treating the symptoms while making the disease worse.
I love knights-and-knaves puzzles: where knights always tell the truth, and knaves always lie. The following puzzle has a new type of person: a sophist. A sophist only makes statements that, standing in their place, neither a truth-teller nor a liar could make. For example, standing next to a liar, a sophist might say, "We are both liars." Think about it. If the sophist was a truth-teller, then the statement would have been a lie, thus creating a contradiction. If the sophist was a liar, the statement would be true, again creating a contradiction.
Here is the puzzle with sophists. And by the way, this one is intended for sixth graders.
Puzzle. You are on an island inhabited by knights, knaves, and sophists. Once upon a time, a sophist made the following statements about the island's inhabitants:
1. There are exactly 25 liars on this island.
2. There are exactly 26 truth-tellers on this island.
3. The number of sophists on this island is no less than the number of truth-tellers.
How many inhabitants were on the island once upon that time?
I love this new sophist character in logic puzzles, but I have no clue why they are called sophists. Can anyone explain this to me?
As my readers know, I collect Russian license plates. They are actually American plates, but the letters form words readable in Russian. This is possible because the shapes of English and Russian letters overlap. Here is my new favorite plate. It is actually not the best plate, but rather makes the best picture ever.

The plate says Moscow, the Russian capital. And the car is parked next to the Ukrainian flag. I am from Moscow too, and I too support Ukraine in its war against evil Putin, who wants to restore the Russian Empire. Did you know that now he wants Alaska?
After reading my post, Shapovalov's Gnomes, Grant, one of my readers, directed me to the Brick puzzle from Section 2.3 of Xinfeng Zhou's A Practical Guide to Quantitative Finance Interviews.
Puzzle. Can you pack 53 bricks with dimensions 1-by-1-by-4 into a 6-by-6-by-6 box?
The solution in Zhou's book has some flaws. So I am posting my own solution here.
Solution. We start with a sanity check. The box contains 216 unit cube cells, and 53 bricks would take up 212 cells. So there is no contradiction with the volume. We need to look at something else.
Let's divide the box into 27 smaller 2-by-2-by-2 boxes and color the smaller boxes in a checkerboard manner. We get 13 boxes of one color, say white, and 14 boxes of another color, say black. Whichever way we place a brick inside the original box, it has to cover 2 white cells and 2 black cells. But we have a total of 104 white cells, which is only enough for 52 bricks.
Alexander Gribalko designed a new coin problem, two versions of which appeared at the 43rd Tournament of the Towns. I will start with the easier version.
Problem. Alice and Bob found eleven identical-looking coins; four of them are fake. All real coins weigh the same. All fake coins weigh the same but are lighter than the real ones. Alice offered Bob four specific coins. Before agreeing to take them, Bob wants to ensure they are all real. Can he do so by only using the balance scale twice? He can use any of the eleven coins for weighing purposes.
Surprisingly, the more difficult version has fewer coins.
Problem. Alice and Bob found eight identical-looking coins; three of them are fake. All real coins weigh the same. All fake coins weigh the same but are lighter than the real ones. Alice offered Bob three specific coins. Before agreeing to take them, Bob wants to ensure they are all real. Can he do so by only using the balance scale twice? He can use any of the eight coins for weighing purposes.
The Conway subprime Fibonacci sequence is defined as follows. Start with the Fibonacci sequence 0, 1, 1, 2, 3, 5, …, but before you write down a composite term, divide it by its least prime factor. Thus, the next term after 5 is not 8, but rather 8/2 = 4. After that, the sum gives us 5 + 4 = 9, which is also composite. Thus, you write 9/3 = 3, then 4 + 3 = 7, which is okay since it is prime, then 3 + 7 = 10, but you write 10/2 = 5, and so on. Here is the sequence: 0, 1, 1, 2, 3, 5, 4, 3, 7, 5, 6, 11, 17, 14, 31, and so on.
My coauthors, Richard Guy and Julian Salazar, and I studied this sequence in our paper Conway's subprime Fibonacci sequences, in which we allowed any two integers to be the two starting terms. Our computation showed that for small starting terms, the sequence starts cycling. In our first draft, we had a probabilistic argument as to why the sequence should always cycle. Our argument was the following.
Flawed probabilistic argument. Consider the parity of the numbers in a particular subprime Fibonacci sequence. I will leave it to the reader to see that such a sequence can't have all even numbers. As soon we get to an odd number, the even numbers in the sequence become isolated. Indeed, if two numbers have different parity, the next number must be odd. For subprime Fibonacci sequences, when we add two odd numbers, there is a 50 percent chance that after dividing by 2, the result will be odd. Assuming the result is odd, there a is 25 percent chance the next number will be odd as well. And this pattern continues. Thus, as soon as we get two odd numbers in a row, on average, we expect three odd numbers in a run of odd numbers. Hence, we would expect a typical subprime Fibonacci sequence to have three times as many odd as even numbers.
This means, on average, two consecutive terms sum to an even number half of the time. Therefore, while calculating the next term, we divide by 2 with probability 1/2 and by 3 with probability 1/6. Ignoring larger primes, on average, we expect to have divided by at least 1.698, while the usual Fibonacci growth is only by a factor φ, which is approximately 1.618. We see that the subprime Fibonacci sequence is divided faster than its expected growth rate. Thus, it has to cycle.
However, this argument doesn't work. When we submitted the paper, an anonymous reviewer pointed out that the argument was flawed. Here I want to explain why. I will start with a counterexample suggested by my sons, Alexey and Sergei.
Counterexample. Start with two real numbers. Suppose the sequence is to add the two previous numbers and divide the sum by 1.8 (which is greater than the golden ratio φ). The resulting sequence grows as a geometric progression with ratio 1.07321.
Here is a variation of the above argument.
Counterexample Variation. Suppose we have a sequence where we add the two previous numbers and then divide the sum by 2. We are dividing by a noticeably larger number than the golden ratio. By our flawed argument earlier, the sequence should decrease. But if we start such a sequence with two identical numbers n and n, the sequence will be constant, disproving the argument.
Here is an additional observation. Obviously, whenever we add two numbers and divide the sum by a number bigger than 2, the sequence has to cycle. Indeed, the maximum of two consecutive terms decreases. Can we add probabilities to this argument? Below is the averaging version of this argument for the subprime Fibonacci numbers. Unfortunately, this argument is also flawed.
Another flawed probabilistic argument. We need to show that, on average, at each step, we divide our sum by a number bigger than 2. We can ignore divisions by 2 as they are fine. Let's see what happens with sums that we do not divide by 2. With probability 1/3, we divide them by 3. If not, with probability 1/5, we divide them by 5. Otherwise, with probability 1/7, we divide them by 7. Hence, if we do not divide our sum by 2, then with probability 1/3, we divide it by 3, plus with probability 2/15, we divide it by 5, plus with probability 8/105, we divide it by 7. Thus, on average, if we do not divide the sum by 2, then we divide it by at least 31/352/1578/105 = 2.07.
Counterexample to the second argument. Why is this wrong? Let us, for example, consider a sequence with the following recursions: a2k+1 = a2k + a2k-1. And a2k = (a2k-1 + a2k-2)/x, where x is a very large number. Then on average, we divide the sum by a very large number. Would this sequence converge to zero? If we look at it more closely, the subsequence of odd-indexed numbers increases. So the answer is no.
We found yet another probabilistic argument that the sequences shouldn't increase indefinitely. We are sure that one works. Our anonymous reviewer was happy with it too. You can find the argument in our paper: Conway's subprime Fibonacci sequences.
But I wrote this essay to show how tricky probabilistic arguments can be.
For students applying to PRIMES, we have a question about their research interests. RSI asks a similar question from their applicants.
I am looking at all the submissions, and this essay will help our applicants to get projects that are well-suited for them.
We, at PRIMES and RSI Math, usually have research projects lined up in advance. That means, we are not creating projects to match applicants' requests. We match existing projects to students' backgrounds and interests.
If you are applying to one of these programs, here is my advice.
Don't be too specific about what you want. Suppose you want to study the symmetries of an icosahedron. This request is too narrow: there is a high probability we do not have such a project. How will we match you to a project? Our hope, in this case, is to find clues in your essay. For example, we might discover that you heard a fascinating lecture on icosahedron's symmetries, which is why you requested the topic. In this case, we assume that another fascinating lecture on a different topic might also excite you, and you will be matched with a random project. But if your description is broader, say, if you write that you like group theory or geometry, your match won't be as random.
Specify things you do not want. Given our project distribution, you might not get a project in the area that is your first or even your second choice. On the other hand, if you write to us that you hate geometry, it is very easy to find a project without a geometric component. If there is something you definitely do not want, it is advantageous for you to mention it.
Be precise about your advanced knowledge. For example, linear algebra is one of the most powerful tools in mathematics. Not surprisingly, we often have projects that require a serious background in linear algebra and specifically look for students who know it. Unfortunately, we often receive inadequate descriptions of students' backgrounds. Even if you took a linear algebra course, it might be useful to mention which book you used and how many chapters you covered. This also applies to other advanced topics. An applicant might say they are proficient in cohomologies after half-listening to one half-hour lecture on the topic. This is not proficiency; it only indicates interest. If you claim advanced knowledge, specify the scope. The best way to start is by listing the books you have attempted to read. For each book, describe which chapters you only scanned, which chapters you read and understood, and for which chapters you solved all of the exercises.
Add more information if your first choice is number theory. Almost every year, we have several students requesting number theory. This might be explained by the successes of the Ross and PROMYS summer programs. The graduates from these programs love number theory and have a good number theory background. However, modern number theory is very advanced, and we seldom have these types of projects. So, if number theory is your top choice, there are two things you can do. First, mention your second choice. Second, specify what you like about number theory. For example, if you are into the more abstract parts of number theory, another abstract project might be a good fit.
Describe your priorities in broader terms. It is beneficial for every starting mathematician to figure out the area they like by asking themselves broader questions. If you know the answers to the questions below, it is helpful to write them on the application form.
If you follow my advice, you might get a project that matches your tastes better. Not only that: figuring out the answers to these questions will help you build the life you love.
I recently posted a cute Shapovalov's puzzle about gnomes. Here is another easier gnome puzzle, also by Alexander Shapovalov.
Puzzle. All gnomes are knights or knaves: knights always tell the truth, and knaves always lie. There is a gnome on every cell of a 4 by 4 chessboard. It is known that both knights and knaves are present in this group. Every gnome states, "Among my neighbors, the number of knaves is the same as the number of knights". How many knaves are there, if by neighbors they mean orthogonally adjacent gnomes?
The next gnome puzzle has a different author, Alexander Gribalko. Gnomes in this puzzle are not knights or knaves but rather friendly and polite beings.
Puzzle. Nine gnomes repeated the following procedure three times. They arranged themselves on a 3 by 3 chessboard with one gnome per cell and greeted all their orthogonal neighbors. Prove that not all pairs of gnomes greeted each other.
Here is another lovely problem from a prolific problem writer, Alexander Shapovalov.
Problem. Every cell of a 7 by 7 chessboard has a gnome standing on it. For every pair of gnomes whose cells share an edge, their beards' lengths differ by no more than 1 inch. Now, we take these gnomes and sit them around a table. Prove that we can do so in a way that any two gnomes sitting next to each other have their beards' lengths differ by no more than 1 inch.
A standard chessboard is 8 by 8. Why would this problem have a 7 by 7 board? Let's see.
For even-sized boards, the problem is easy. I will explain why, but first, let me construct a graph related to a board, in this case, any board.
Each cell is a vertex, and two vertices are connected by an edge if the corresponding cells are orthogonal neighbors (share an edge) on the board. A cycle that goes through a graph and visits every vertex exactly once is called a Hamiltonian cycle. A Hamiltonian cycle is a potential way to sit the gnomes around the table and solve the problem. When we sit the gnomes in a circle following a Hamiltonian cycle, two neighbors at the table are also neighbors on the board, and so they have their beards' lengths differ by no more than 1 inch.
The problem is easy for even-sized boards because it is easy to draw a Hamiltonian cycle on them. An odd-sized chessboard can't have a Hamiltonian cycle. To prove this, let me color the board in a checkerboard manner. Then, cells that share an edge are different colors. And you can't make a cycle through the board, where you switch colors at each step, but the total number of steps is odd.
It follows that for odd-sized boards, it is impossible to solve the problem by just connecting neighboring cells on the board. There should be another way. Can you find it?
I want to discuss a problem from a test I gave recently.
Problem. My dog, Fudge, likes books. He brought two books to his corner in the morning and three more books in the evening. How many books will he read tonight?
As I expected, many students didn't pay attention and just summed up the two numbers in the problem and gave five as the answer. Here are three answers that I especially liked.
Answer 1. Zero, because most dogs can't read.
This cautious student added most to be on the safe side.
Answer 2. You cannot tell how many books he will read. Just because he brings books to his corner doesn't mean he will read them.
The second answer demonstrates great logical thinking, were Fudge a human. But the third answer made me laugh.
Answer 3. Three. If he brought three more books to his corner in the evening, it means he finished the two from that morning, so there are three books left for him to read.
Thinking about genders, we used to have only two options: male and female. Now we have more. I have a lot of young acquaintances who are non-binary. So I started to rethink my gender identity.
I was a typical girl: at least, I thought I was. I hated playing with boring dolls. I preferred cars, or even better, construction sets and board games. In second grade, I wanted to be a ballerina but later fell in love with Sherlock Holmes. My dreams switched to becoming a detective or a spy. In fifth grade, I signed up for rifle-shooting training. That same year, my school forced me to compete in an orienteering event, and I won.
Orienteering became my favorite sport, and I did it for many years. I was really good with maps. I would go to a competition, leisurely walk my course and win. Other kids were running around like crazy, but I always knew where to go and was overall faster than them. With time, other kids learned to read maps better, but I myself never learned to run faster. So I stopped winning, but I enjoyed the sport anyway.
It goes without saying: I loved math. Solving math problems was the best entertainment ever.
Later, to my surprise, I discovered that most girls liked shopping and wasted a lot of time on make-up. Not many girls were even interested in math. I actually liked that. I started having crushes on boys since second grade and enjoyed being the only girl in math clubs, having all these nerds to myself.
I grew up in Soviet Russia. While growing up, I wasn't bombarded with gender stereotypes. My first eye-opening experience was when I was 17 years old. My long-time boyfriend knew that I liked mathematics, and this was okay. But when I told him that I planned to go to college to study mathematics, he didn't approve. I broke up with him on the spot.
My mom used to tell me that most men do not like brainy women. My reply was that there are more men who like brainy women than brainy women. I got a new boyfriend the day after my breakup.
My gender identity didn't bother me much in Russia. What bothered me was the Russian tradition for both spouses to work, but the house chores and child-rearing duties fell only on women. I read somewhere that, on average, in Russia, women worked for 4 hours a day more than men. Life was unfair to women but not to their self-esteems.
As I said, I grew up thinking I was a typical girl until I came to the US. This happened 30 years ago, and I was 30 at the time. In the US, I got bombarded with gender stereotypes: they made me feel inadequate and doubt my femininity. Just for reference: by that time, I was in my third marriage breastfeeding my second child. Still, according to those stereotypes, I was not a real woman.

For some time, I wondered what was wrong with me. Then, I was elated to find a book called Brain Sex: The Real Difference Between Men and Women by Anne Moir and David Jessel. (This was many years ago.) Among other things, this book talks about the differences between men and women with respect to the brain. According to the book, men are better on average at abstract thinking and spatial visions, aka math and maps. Women, on the other hand, are better at connecting with people and have higher social intelligence. Boys are less interested in games related to storytelling, aka dolls, preferring more concrete activities. And so on.
The book also describes situations in which girls don't fit the paradigm. The authors attribute this variation to the mother's hormones during pregnancy. I found myself described perfectly in the section titled "girls who have been exposed to male hormones in the womb." I am pretty sure that my mom didn't take any hormone supplements while pregnant with me back in Soviet Russia. On the other hand, the description in the book was spot-on.
This book classifies me as "a male brain in a female body."
I was glad to find myself after a period of self-doubt. I was glad that I wasn't alone and even fit into a special category with a name.
Several years later, I met Sue Katz, a writer who also has a blog Sue Katz: Consenting Adult. She made me realize how ridiculous the whole story was: I was pressured by gender stereotypes to feel bad about myself. Then I was grateful for a book based on those same stereotypes, only because it described women like me and gave me permission to exist. I liked the book because I accepted those stereotypes in the first place. If there were no stereotypes, there wouldn't be any problems at all.
Why can't I just be me?
Over the past few years, I have become happier than I have ever been. I do not care what society thinks about my gender. I am no longer ashamed of not feeling 100 percent female.
I like that people in the modern world embrace the idea of individuals being themselves. For example, my daughter-in-law, Robin Dahan, designed a whole line, You-Be-You, for her company, Dash of Pep.

Am I non-binary? I do not know and do not care. I am just me, proudly wearing my You-Be-You socks.
Assume that we have n men and n women, all of whom want to get married. They rank each other without ties. After that, we can match them into n pairs for marriage. The matching is called stable if there are no rogue couples. A rogue couple is defined as a man and a woman who prefer each other over their assigned future spouses.
A famous theorem says that, whatever all the rankings are, a stable matching always exists. But how good could a stable matching be? There is a way to assign a quality score to a matching, called the egalitarian cost. The egalitarian cost of any matching is the sum of the rankings that each person gave their assigned partner. The best potential outcome is when all people are matched with their first choices. This corresponds to the minimum egalitarian cost of 2n. But what is the maximum egalitarian cost of a stable matching? I couldn't find it in the literature, so I proved that it is n(n+1).
Proof. It is easy to see that the egalitarian cost of n(n+1) is achievable. For example, if all men gave an identical ranking to the women, and vice versa, the matching algorithm will end up with couples having mutual rankings (j,j) for different values of j. Another example is a Latin preference profile. Each woman ranks a man n+1−x whenever he ranks her x. In this case, every potential couple's mutual rankings sum to n+1. Thus, any matching for such rankings ends up with the egalitarian cost of n(n+1).
The next step is to prove that the egalitarian cost can't be greater. Suppose the cost of a stable matching is C and is greater than n(n+1). Then, for every person, we count the number of people who are better (ranked smaller) than their assigned partner and sum these numbers over all the people. The result must be C−2n, which is the number of pairs of people of opposite genders such that the first person prefers the second one over their assigned partner. Moreover, the result is greater than n(n−1).
The total number of possible couples is n2. Thus, the number of unrealized potential couples is n(n−1). We can conclude that we counted one of these unrealized couples twice. In such a couple, two people prefer each other over their assigned partners. Thus, they form a rogue couple, contradicting our assumption that the matching is stable.
Here is an old goodie.
Puzzle. A criminal is sentenced to death. He is offered the last word. He is allowed to make one statement. If the statement is true, the criminal will be electrocuted. If the statement is false, he will be hanged. Can you find a good piece of advice for this man?
The standard answer to this puzzle is for the criminal to say, "I will be hanged." This creates a paradox. If he is hanged, the statement is true, and he should be electrocuted. If he is electrocuted, the statement is false, and he should be hanged.
Thinking about it, any paradox works. If the man says, "This statement is false," then the type of punishment he gets can't be determined.
Thinking about it some more, asking a question instead of making a statement will confuse his executioners all the same.
One of my students advised the criminal to stay silent. This was not my favorite solution, as staying silent requires some concentration. My favorite solution was the statement, "It will rain exactly a thousand years from now." This way, the criminal can relax, at least for a thousand years.
Today I discuss ideas for solving the puzzle I posted previously in my blog: A Scooter Riddle.
Riddle. Alice, Bob, and Charlie are at Alice's house. They are going to Bob's house, which is 33 miles away. They have a 2-seat scooter that goes 25 miles per hour with 1 rider, or 20 miles per hour with 2 riders. Each of the 3 friends has a walking pace of 5 miles per hour. What is the fastest time that all three of them can end up at Bob's house?
Let's start.
Now this is just algebra. Each person covers 20x miles on the scooter and 33 − 20x miles on foot. The walking takes 33/5 − 4x hours. Thus the total trip for each person takes 33/5 − 3x hours.
Now we calculate what the scooter does. The scooter covers 20x miles with Alice and the same number of miles with Bob. It covers 40x − 33 miles alone. Thus the scooter spends 2x + (40x − 33)/25 hours in transit. The two times must be the same. So we have an equation: 6.6 − 3x = 2x + 1.6x − 1.32. Thus, x = 1.2, and the answer to the puzzle is 3 hours.
If you can figure out my number without the Internet, call me.
(Just in case: this is a joke and not my actual phone number.)

This is my second crocheting project to help finance our new program, Yulia's Dream, in honor of Yulia Zdanovska, a young Ukrainian math talent killed in the war.
I made four Whitehead links in the colors of the Ukrainian flag. You can read about my other crocheting project in my previous post: Hyperbolic Surfaces for Ukraine.
Fun trivia about the Whitehead links.

As you might know, my team started a project, Yulia's Dream, in honor of Yulia Zdanovska, a young Ukrainian math talent killed in the war.
In this program, we will do what we are great at — help gifted youngsters pursue advanced math. To help the program, I started crocheting hyperbolic surfaces in the colors of the Ukrainian flag. These crochets are designed as gifts to encourage individual donors.
Fun trivia about these hyperbolic surfaces.
Overall, I crocheted 10 hyperbolic surfaces. If you are interested in donating to help Ukrainian students receive coaching from our program at MIT, the details will be announced on our website shortly.
What is base 3/2? One of the ways to define such a base is to think of it in terms of exploding dots. What the heck are exploding dots? They are explained and popularized by James Tanton in his YouTube videos.
Essentially, "exploding dots" is a machine made of a row of boxes with rules describing how the dots loaded into the machine explode. As an example, let me describe the 1←2 machine, which corresponds to base 2. We load N dots into the rightmost box. Whenever there are 2 dots in one box, they explode into 1 dot in the box to the left.
For example, to write 5 in base 2, we would first load 5 dots in the rightmost box, as in the figure above. Then each group of 2 dots in the rightmost box would explode, and for each group, 1 dot would appear in the box to the left. Finally, the 2 dots in the second box would explode into 1 dot into the next box to the left. By reading the number of dots from left to right, we get 101, which is 5 in base 2.
The interesting thing here is that there is no reason this model should be exclusive to integer bases. Suppose our rule is that 3 dots explode into 2 dots in the box to the left. Such a rule is called the 2←3 machine, and it corresponds to base 3/2. To represent 5 in this base, we load 5 dots into the rightmost box, then we use the exploding rule shown in the figure below. Using this machine, 5 is represented in base 3/2 as 22.
The figures were made by my junior PRIMES STEP group, in the 2017-2018 academic year, for our paper, Variants of Base 3 Over 2.
But, in this post, I want to discuss a different paper from the same academic year. With my senior PRIMES STEP group, we wrote a paper On Base 3/2 and its Sequences. A shorter version which includes a tribute to John Conway, appeared in The Mathematical Intelligencer.
Speaking of John Conway, he liked inventing new sequences, especially ones with unusual behaviors. One of his hobbies was tweaking the Fibonacci rule to create new sequences, which he called Fibs. For example, the sorted Fibs sequence starts the same as the Fibonacci sequence with 0 and 1. To calculate the next term, we add the two previous terms and sort the digits in non-decreasing order. In base 10, this sequence is A069638: 0, 1, 1, 2, 3, 5, 8, 13, 12, 25, 37, 26, …. It is known that this sequence is periodic with a maximum value of 667.
With my senior PRIMES STEP group, we studied analogs of this sequence in base 3/2. We begin with the sorted Fibs sequence fn with the same two initial values that start the Fibonacci sequence: f0 = 0 and f1 = 1. To calculate fn+1, we add fn-1 and fn in base 3/2 and sort the digits in non-decreasing order. It follows that the numbers in the sequence are written as several ones followed by several twos. Unlike base 10, the sequence is not periodic and grows indefinitely: 0, 1, 1, 2, 2, 12, 12, 112, 112, 1112, 1112, 11112, …. In recognition of the constant growth of this Fibs sequence, we call it the Pinocchio sequence.
Obviously, you can start the sorted Fibs sequence with any two numbers. But we proved an interesting theorem which stated that any sorted Fibs sequence eventually turns into either the tail of the Pinocchio sequence or the 3-cycle 112, 1122, 1122.
However, we didn't stop there. There are two natural ways to sort the digits of a number, in increasing or decreasing order. Naturally, there is another type of sequences worth considering, in which the digits are sorted in non-increasing order. We called such sequences the reverse sorted Fibs.
We defined the reverse sorted Fibs sequence rn in base 3/2 as follows. To calculate rn+1, we add rn-1 and rn in base 3/2 and sort the digits in non-increasing order, ignoring zeros. It follows that after the initial terms, the terms of such a sequence are represented with several twos followed by several ones. We call the reverse sorted Fibs that start in a similar way to the Fibonacci sequence with r0 = 0 and r1 = 1, the proper reverse sorted Fibs. Here are several terms of the proper reverse sorted Fibs: 0, 1, 1, 2, 2, 21, 21, 221, 2211, 221, 221, 2211, 221, 221, 2211, …. This sequence becomes cyclic, starting from r7.
We also found one reverse sorted Fibs growing indefinitely: 2211, 2211, 22211, 22211, 222211, 222211, and so on. We proved that any reverse sorted Fibs sequence eventually turns into either this sequence or a 3-cycle sequence: 221, 221, 2211. The similarity between the sorted Fibs and the reverse sorted Fibs surprised us. Up to the initial terms, they both have exactly one sequence which grows indefinitely and one 3-cycle. To emphasize this similarity, we reversed the word Pinocchio and named this growing reverse Fibs sequence the Oihcconip sequence.
Now I need to figure out how to pronounce the name of this new sequence.
I run Number Gossip, where you can input a number and get some of its cute properties. For example, the number 63 is composite, deficient, evil, lucky, and odd. In addition, it has a unique property: 63 is the smallest number out of two (the other being 69), such that the common alphabetical value of its Roman representation is equal to itself. Indeed, the Roman representation of 63 is LXIII, where L is the 12th digit, X is the 24th, and I is the 9th. Summing them up, we get 12 + 24 + 9 + 9 + 9 = 63 — the number itself.
I have a list of about 50 properties of numbers that my program checks. Each number greater than one gets at least four properties. This is because I have four groups of properties that cover all the numbers. Every number is either odd or even. Every number is either deficient, perfect, or abundant. Every number greater than one is either prime or composite. Every number is either evil or odious.
In addition, I collect unique number properties. During the website's conception, I decided not to list all possible unique properties that I could imagine but to limit the list to interesting and unusual properties. My least favorite properties of numbers are the ones that contain many parameters. For example, 138 is the smallest number whose base 4 representation (2022) contains 1 zero and 3 twos. If you are submitting a number property to me, keep this in mind.
Some parameters are more forgiving than others. For example, 361 is the smallest number which is not a multiple of 9, whose digital sum coincides with the digital sum of its largest proper divisor. In more detail, the digital sum of 361 is 3 + 6 + 1 = 10, while 19, the largest divisor of 361, has the same digital sum of 10. In this case, the parameter 9 is special: for a multiple of 9, it is too easy to find examples that work, such as 18, 27, and so on. Sequence A345309 lists numbers whose digital sum coincides with the digital sum of their largest proper divisor. The first 15 terms of the sequence are divisible by 9, and 361 is the smallest term that is not divisible by 9.
By the way, another number that is buried deep in a sequence is 945, which is the smallest odd abundant number. There are 231 abundant numbers smaller than 945; all of them are even.
A more recent addition to my collection is related to the sequence of distended numbers (A051772). Distended numbers are positive integers n for which each divisor of n is greater than the sum of all smaller divisors. It is easy to see that for distended numbers, all sums of subsets of divisors are distinct. The opposite is not true: 175 is the smallest number, where all sums of subsets of its divisors are distinct, but the number itself is not distended.
It is difficult to find special properties for larger numbers, so I am less picky with them. For example, 3841 is the number of intersections of diagonals inside a regular icosagon. The word icosagon hides a parameter, but I still like the property.
I invite people to submit number properties to me. And I received many interesting submissions. For example, the following oxymoronic property was submitted by Alexey Radul: 1 is the only square-free square.
The numbers below 200 that still lack unique properties are 116, 147, 155, 162, 166, 182, and 194. The earliest century that doesn't have unique number properties ranges between 7000 and 7100. The next ones are 8000–8100 and 9100–9200. By the way, my site goes up to ten thousand.
I also have a lot of properties in my internal database that I haven't checked yet. I am most interested in the proof of the following property: 26 is the only number to be sandwiched between any two non-trivial powers.
One of my posts about John Conway has a picture I took of him in 2015, leafing through a book about himself, Genius at Play. I allowed Wikipedia to use this image, and they did. They also retouched it for their article on John Conway in Dutch. I like the result.


Every year, after the MIT Mystery Hunt was over, I would go through all the puzzles and pick out the ones related to mathematics. This year, I didn't feel like doing it. Besides, I think it is more important to collect quality puzzles rather than all the puzzles by topic. So my new collection is the puzzles recommended to me, which I might like.
I start with math and logic puzzles.
I continue with computer science.
I carry on with some non-math fun.
I conclude with the plot device round. All the puzzles in this round are relatively easy. But our team got stuck on them until we realized that we already had the answer, which was not a single word. Here are some of the puzzles that were specifically recommended.
Putin became the 21st century Hitler. I call him Putler.
I am an American. However, I was born in Moscow and lived my youth in the Soviet Union. I speak Russian, and I have friends in both Russia and Ukraine. The war in Ukraine is the biggest tragedy of my life.
When Putler invaded Ukraine, I didn't know what to do. I wanted to pick up a rifle and go to Ukraine to fight, but then I remembered my CPAP machine and the distilled water it needs, and I didn't go. Instead, I ended up watching the news non-stop. Then I started sending money to different organizations supporting Ukraine.
However, I am a mathematician, so I tried to figure out whether I could help Ukraine by doing math. At first, I posted math problems from Ukraine Olympiads. Then I started discussing what we could do with my PRIMES colleges. The result was a new program, Yulia's Dream, in honor of Yulia Zdanovska, a 21-year-old brilliant young Ukrainian mathematician killed by a Russian-fired missile. Yulia's Dream is a free enrichment program for high-school students from Ukraine who love math.
All these activities didn't help me with the pain. So I started crocheting. I bought yarn in the colors of the Ukrainian flag and crocheted a hyperbolic surface of constant curvature. The first picture shows the thingy from above. The second one is there for you to estimate its size: this is the biggest crocheting project I have ever finished.


For a free Ukraine! Let democracies win over dictatorships!
I wrote a lot about how during entrance tests for Moscow State University, the examiners were giving Jewish and other undesirable students special (e.g. more difficult) questions during the oral exams. (See, for example, our paper Jewish Problems with Alexey Radul.) Not all examiners agreed to do this. So the administration made sure that there were different exam rooms: brutal rooms with compliant examiners torturing students with difficult questions, and normal rooms with normal examiners testing preapproved students. The administration also had other methods. One of them is the topic of this essay.
The math department of Moscow State University had four entrance exams. The first was a written math test consisting of three trivial problems, a very difficult one, and a brutally challenging one. At the end, I will show you a sample: a trivial problem and a very difficult one from 1976, my entrance year.
What was the point of such vast variation in difficulty, you may ask? There were two reasons.
But first, let me explain some entrance rules. The exam was scored according to the number of solved problems. A score of two or less was a failing score. People with such scores would be disqualified from the next exam. Any applicant with a smidge of mathematical intelligence would be able to solve all three trivial problems. Almost all applicants who qualified for the next test would have the same score of three on the first test, as they wouldn't be able to solve the last two problems. Thus, mathematical geniuses and people who barely made the cut got the same score.
There was another rule. Officially, people with a gold medal from their high school (roughly equivalent to a valedictorian) could be accepted immediately if they scored 5 on the first exam. So one of the administrative goals was to prevent anyone getting a 5, thus, blocking Jewish applicants from sneaking in after the first exam.
Another goal was to have all vaguely qualified people get the same score. The same goal applied to other exams. After the four admission exams, the passing score, say X, was announced. A few people with a score higher than X were immediately accepted. Then there were hundreds of applicants with a score of X, way more than the quota of people the department was planning to accept. An official rule allowed the math department to pick and choose whoever they wanted from everyone who scored X.
I heard a speech by the famous Russian mathematician, Vladimir Arnold, directed at decent examiners who tested "approved" students at the oral math exam, which was the second admissions exam. His suggestion was brilliant and simple. If the students are good and belong in the department, give them an excellent grade of 5. If not, give them a failing grade of 2. Arnold's plan boosted the chances of good students doing better than the cutoff passing score X and removed mediocre students from the competition. His idea was not only brilliant and simple but also courageous: he was risking his career by trying to fight the system.
I never experienced the entrance exams firsthand. By ministry order, as a member of the USSR IMO team, I was accepted without taking any exams. I already wrote an essay, A Hole for Jews, about how getting on the IMO team was the only way for Jewish students to get into the Moscow State University, and how the University tried to block them.
But I still looked at the entrance exam problems I would have had to solve to get in. The last two problems scared me. Now I found them again online (in Russian) at: the 1976 entrance test. The trivial problem below is standard and mechanical, while the other problem still looks scary.
Trivial problem. Solve for x:
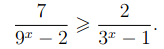
Solution. We were drilled in school to solve these types of problems, so this one was trivial. First, make a substitution: y = 3x. This leads to an equation: (2y - 1)(y - 3)/(y2 - 2)(y - 1) ≤ 0. From this we get ranges for y: (-∞, -√2], [1/2,1], [√2, 3]. The last step is to take a logarithm.
Very difficult problem. Three spheres are tangent to plane P and to each other. Two of the spheres are the same size. The apex of a circular cone is on P, and the cone's axis is perpendicular to the plane P. All three spheres are outside the cone and tangent to it. Find the cosine of the angle between the cone's generatrix and the plane P, if one of the angles of the triangle formed by the intersection points of the spheres and the cone is 150 degrees.
I stumbled upon one of Smullyan's puzzle on Facebook, in Russian. I couldn't find the original text, so I just translated it back for my students.
Puzzle. You are on an island where only truth-tellers and liars live. The truth-tellers always tell the truth, and the liars always lie. You meet an islander who sits with you for a long time, then says, "I already said this sentence." Is he a truth-teller or a liar?
I expected the following solution. If this islander is a truth-teller, then there should have been a time when he said, for the first time, "I already said this sentence." But this would create a contradiction.
However, my students used this puzzle as an opportunity to teach me some intricacies of the English language. They explained to me the ambiguities of my translation. Here is a shortened and lightly edited quote from one of them:
There are two different linguistic opinions that give different answers to this problem. The first is that the truth of a statement is decided at the moment it starts to be delivered: in this case, when the islander starts saying his statement. With this interpretation, for the statement to be true, he had to have said the sentence before, and for that to be true, he had to have said it even before that, and this continues indefinitely. Clearly, he cannot have been alive forever, so he has to be a liar.
The other opinion is that the verity of a statement is decided at the exact conclusion of its deliverance. Then, when the islander finishes saying his sentence, its truth is judged, and he has at that same instant "already" said the sentence, so he is telling the truth. By this interpretation, the islander is a truth-teller.
Another student had a different brilliant idea. Depending on the islander's intonation, it is possible that he says, "I already said 'this sentence'." In that case, there are no self-referencing sentences, and the islander could be either a truth-teller or a liar.
I consulted my best English consultant: my son, Alexey, and here is his reply. "The basic answer is that neither truth nor semantic meaning are absolute, and edge cases will be judged differently by different observers. A sentence whose truth is time-dependent on the same scale as the duration of uttering the sentence is clearly an edge case. That's why mathematicians intentionally try to eliminate ambiguity from their communication."
He suggested the following fix for the puzzle's translation.
Fixed puzzle. You meet an islander who says, "I have said this sentence before." Is he a truth-teller or a liar?
Alexey didn't stop at fixes and suggested the following bonus puzzles.
Bonus puzzle 1. You meet an islander who says, "I will have said this sentence." Is he a truth-teller or a liar?
Bonus puzzle 2. You meet an islander who says, "I will say this sentence again." Is he a truth-teller or a liar?
Ukraine is on my mind. Here is a problem for 9-graders from the 1978 Ukrainian Math Olympiad:
Problem. Prove that for every natural number n, the following number is not an integer.
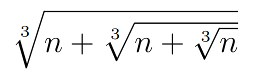
Oskar van Deventer is a designer of beautiful mechanical puzzles. For the recent mini-MOVES gathering at the MoMath, he asked people in his Zoom breakout room to calculate the average age in the room without revealing their actual ages. I know the following solution to this puzzle.
People agree on a large number N that is guaranteed to be greater than the sum of all the ages. The first person, say Alice, thinks of a uniformly random integer R between 0 and N. Alice adds her age to R modulo N and passes the result to the second person, say Bob. Bob adds his age modulo N and passes the result to the third person, and so on. When the result comes back to Alice, she subtracts R modulo N and announces the sum total of all the ages.
During this process, no one gets any information about other people's ages. But two people can collude to figure out the sum of the ages of the people "sitting" between them.
I gave this problem to my grandson, and he suggested the following procedure. First, people choose two trusted handlers: Alice and Bob. Then, each person splits their age into the sum of two numbers (the splitting should be random and allow one of the numbers to be negative). They then give one number to Alice and another to Bob. Alice and Bob announce the sums of the numbers they receive. After that, the sum total of everyone's ages is the sum of the two numbers that Alice and Bob announce.
The advantage of this method is that no two people, except Alice and Bob, can collude to get more information. The disadvantage is that if Alice and Bob collude, they would know everyone's age. Which method would you prefer?
Many years ago, I wrote a blog post about an amusing fact: John Conway put Moscow, the former capital of the USSR, as a coauthor: A Math Paper by Moscow, USSR. Thus, Moscow got an Erdős number 2, thanks to Conway's Erdős number 1. At that time, my Erdős number was 4, so I wondered if I should try coauthoring a paper with Moscow, my former city of birth, to improve my Erdős number.
This weird idea didn't materialize. Meanwhile, my Erdős number became 2 after coauthoring a paper with Richard Guy, Conway's Subprime Fibonacci Sequences. I relaxed and forgot all about my Erdős status. I couldn't do better anyway, or could I?
I recently heard about a cheater who applied to grad schools. In addition to a bunch of fabricated grades, the cheater submitted an arXiv link to a phony paper. What is fascinating to me is that the cheater put real professors' names from the university the cheater supposedly attended as coauthors. The professors hadn't heard of this student and had no clue about the paper. So the cheater added fake coauthors to add legitimacy to their application and boost the perceived value of the cheater's "research". As a consequence, the cheater got a fake Erdős number.
I hope that the arXiv withdrew the paper. Cheating is the wrong way to improve one's Erdős number.
But here is another story. Robert Wayne Thomason named as coauthor his dead friend, Thomas Trobaugh. The paper in question is Higher Algebraic K-Theory of Schemes and of Derived Categories and can be found at https://www.gwern.net/docs/math/1990-thomason.pdf. This paragraph in the paper's introduction explains the situation.
The first author [Robert Wayne Thomason] must state that his coauthor and close friend, Tom Trobaugh, quite intelligent, singularly original, and inordinately generous, killed himself consequent to endogenous depression. Ninety-four days later, in my dream, Tom's simulacrum remarked, "The direct limit characterization of perfect complexes shows that they extend, just as one extends a coherent sheaf." Awaking with a start, I knew this idea had to be wrong, since some perfect complexes have a non-vanishing K0 obstruction to extension. I had worked on this problem for 3 years, and saw this approach to be hopeless. But Tom's simulacrum had been so insistent, I knew he wouldn't let me sleep undisturbed until I had worked out the argument and could point to the gap. This work quickly led to the key results of this paper.
This precedent gives anyone hope that they might achieve an Erdős number 1. You just need to wait for Paul Erdős to come to you in your dreams with a genius idea.
Last year, our junior PRIMES STEP group studied Latin squares. We invented a lot of different types of Latin squares and wrote a paper about it, Fun with Latin Squares. Recall that a Latin square is an n by n table containing numbers 1 through n in every cell, so that every number occurs once in each row and column. In this post, I want to talk about anti-chiece Latin squares.
First, what's a chiece? A chiece is a portmanteau word made out of two words, chess and piece, and, not surprisingly, it means a chess piece. Given a chiece, an anti-chiece Latin square is a Latin square such that any two cells, where our chiece can move from one cell to the other, according to the rules of chess, can't contain the same number. Let's see what this means.
Let's start with rooks, which move along rows and columns. An anti-rook Latin square can't have the same numbers repeating in any one row or column. Ha, anti-rook Latin squares are just Latin squares. Anti-bishop and anti-queen Latin squares can't have the same numbers repeating on any diagonal.
Now, here is a picture of an anti-knight Latin square in which no two identical numbers are a knight's move apart. This particular Latin square also forms a mini-Sudoku: not only does each row and column, but also each 2 by 2 corner region, contains all distinct numbers.
Consider all instances of some number, say 1, in an anti-chiece Latin square. If the board is n by n, we get n instances of non-attacking chieces. A famous math puzzle asks to place eight non-attacking queens on a standard chessboard. So the instances of any one particular number in an anti-queen Latin square solves the problem of placing n non-attacking queens on an n by n chessboard. Thus, building an anti-queen Latin square is more complicated than solving the non-attacking queens puzzle. The former requires filling the chessboard with n non-overlapping sets of non-attacking queens. The picture below gives an example of an anti-queen 5 by 5 Latin square.

This square has some interesting properties. It can be formed by cycling the first row. It also happens to be one of the chiece Latin squares we study in our paper. A chiece Latin square is a Latin square such that for each number in a cell, there is another cell, a chiece's move apart, containing the same number. You can check that our anti-queen Latin square is at the same time a knight Latin square.
I wonder, can anyone build an anti-queen Latin square on the standard 8 by 8 chessboard?
Here is the famous barber paradox.
Paradox. The barber shaves all those and only those who don't shave themselves. Does the barber shave himself?
If he shaves himself, then he doesn't shave himself. If he doesn't shave himself, then he shaves himself.
English is not my primary language, and I am fascinated by the variety of verb tenses in English as compared to the Russian language. For example, Russian has one present tense while English has four. I wonder what would happen if we use the other present tenses in this paradox.
Present continuous. The barber shaves all those and only those who aren't shaving themselves. Does the barber shave himself?
Does this mean that the barber starts shaving himself and then has to stop, and a moment later he has to start again?
Present perfect. The barber shaves all those and only those who haven't shaved themselves. Does the barber shave himself?
Does this mean that the barber shaves himself every other day?
Present perfect continuous. The barber shaves all those and only those who haven't been shaving themselves. Does the barber shave himself?
Does this mean the barber shaves himself once in his lifetime and then never again?
Gowers starts with several assumptions.
From these assumptions, the following theorem can be deduced.
Theorem. The only possible rule satisfying these assumptions would allow any two people to have sex with each other as long as they both reached some fixed age k.
There is a problem with this type of rule. Suppose k is 18. If two people who are slightly younger than 18 have consensual sex, they can't both be predators. These are two children with raging hormones. There is no reason to punish anyone. Now imagine that one of the partners turns 18. Society would still consider this a Romeo-and-Juliet case and would tend not to punish such a partner. Now imagine a child younger than 18 having sex with a partner over 40. The older partner has no raging hormones, knows what they are doing, and probably knows how to manipulate little children into having sex. So, it might be desirable to have a rule that differentiates between these two cases. The rule would take into account the difference in ages while forgiving younger offenders and still punishing predators.
Consider the most common type of law to resolve this issue: Anyone older than 18 can have sex, and, in addition, a person who is not older than 20 can have sex with someone between the ages of 16 and 18. This law doesn't satisfy monotonicity. It could be that one day the older partner is not yet 20, and the next day, oops, they have a birthday. So, as a birthday gift, they are not allowed to have sex with each other anymore.
Here is a simple idea to resolve the issue by having the law focus on the age gap instead of the age of the older partner. We can have an adjusted law: Anyone older than 18 can have sex, and, in addition, a person can have sex with someone between the ages of 16 and 18 as long as the age gap is not more than four years. This rule doesn't satisfy the simplicity assumption above, but it is simple enough. It is close in spirit to the previous rule and satisfies monotonicity. The problem with this rule is continuity.
According to the adjusted rule, the couple with the age gap of four years and one day might have to wait two years longer to have sex than the couple with the age gap of four years. This seems unfair.
Tim Gowers suggests dropping the simplicity rule. We can use days rather than years. For example, the rule might be that if one person in a couple is under 18, but at least 16, and has age x, then the other partner has to be not more than age y, where for example, y − x = 4 + (x − 16)/2. So when one partner turns 16, their partner has to be not older than 20. When one partner is 16 and two months, the other cannot be older than 20 and three months. With the younger partner getting older, the allowable age gap is increasing slowly. By the time the younger partner is a day from turning 18, their partner can be almost five years older.
It might be complicated for two people to calculate if they are allowed to have sex according to this formula. But Gowers' big idea was that apps and websites could do this easily: two people plug in their birthdays and know whether they are allowed to have sex.
Do you know what an isosceles tetrahedron is? I didn't until recently. An isosceles tetrahedron has all of its faces congruent. Equivalently, all pairs of opposite edges are of equal length. Such tetrahedra are also called disphenoids. Here are some cute statements about them.
Disphenoids have three nontrivial symmetries: 180-degree rotations around three lines connecting the midpoints of opposite edges.
Is it possible to have a tetrahedron with fewer symmetries than disphenoids? Yes, it is. Dan Klain just published a fascinating paper about such tetrahedra: Tetrahedra with Congruent Face Pairs. The results are so elegant and simple that I was surprised that they were new. I got curious and started to google aggressively. I found an official name for this kind of tetrahedron: phyllic disphenoid, but no theorems about them. Their name is quite unappealing: no wonder people didn't want to study them much. Obviously, Dan wasn't as aggressive at googling, so he didn't find this official name and called them reversible tetrahedra. But my favorite name for them is the name Dan thought of but didn't use in his paper: bi-isosceles tetrahedra.
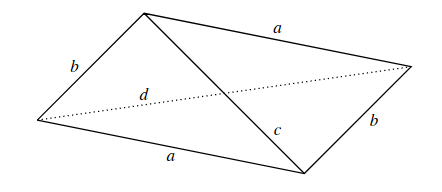
Here is the picture of a bi-isosceles tetrahedron from Dan's paper. It has two faces with sides a, b, and c, and two faces with sides a, b, and d. The edges of this tetrahedron are: a, a, b, b, c, and d. It has one nontrivial symmetry: a 180-degree rotation around the line connecting the midpoints of the unequal opposite edges c and d. The picture emphasizes this symmetry. The figure in the picture is a projection of a bi-isosceles tetrahedron onto a plane, such that the line of symmetry is projected onto the point of symmetry of the projection. The two cute statements above, about disphenoids, can be generalized to the case of bi-isosceles tetrahedra.
The first property is trivial, while the second one is proven in Dan's paper. Dan also shows how to calculate the volume of a bi-isosceles tetrahedron:
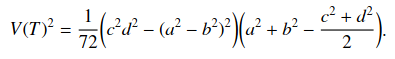
Here is a problem from the 1978 Kyiv Olympiad for 7 graders.
Is it possible to place seven points on a plane so that among any three of them, two will be at distance 1 from each other?
Puzzle. Two girls were born to the same mother, at the same time, on the same day, in the same month, in the same year, and yet somehow they're not twins. Why not?
I won't tell you the expected answer, but my students are inventive. They suggested all sorts of scenarios.
Scenario 1. There are two different fathers. I had to google this and discovered that, indeed, it is possible. This phenomenon is called heteropaternal superfecundation. It happens when two of a woman's eggs are fertilized by sperm from two different men. Unfortunately for my students, such babies would still be called twins.
Scenario 2. The girls are born on the same date, but not on the same day. This could happen when transitioning from the Julian to Gregorian calendar. The difference in birth times could be up to two weeks. I had to google this and discovered that twins can be born months apart. The record holders have a condition called uterus didelphys, which means that the mother has two wombs. Unfortunately for my students, such babies would still be called twins.
Scenario 3. The second girl is a clone. This scenario can potentially happen in the future. Fortunately for that student, I suspect that such babies would be called clones, not twins.
I decided to invent my own scenario outside of the actual answer, and I did.
Scenario 4. Two girls are from the same surrogate mother, but they are not twins. I had to google this and discovered that this actually happened: Surrogate mother of 'twins' finds one is hers.
Sometimes life is more interesting than math puzzles.

In his article on Möbius strips, Martin Gardner included a cute construction.
Construction. Cut out a cross from a piece of paper. Then glue one pair of opposite ends to make a cylinder and the other pair to make a Möbius strip. Then Martin instructs, "Trisect the twisted band, then bisect the untwisted one, and open up for a big surprise!"
In my effort to reuse Möbius strips, I started making them out of zippers. So Martin's construction had its destiny zipped. The first picture shows the construction before it is being dissected. I was quite happy with my plan to use zippers as it had its advantages over paper. For the surprise to work, the twisted band shouldn't be cut completely. Meaning, the middle part of the Möbius strip shouldn't be cut. I sewed my zipper monstrosity not to cause any ambiguities: there is nothing to cut, just unzip the zippers.
Little did I know that unzipping is not the issue, but zipping back up is. I tried to zip the surprise back up several times; all of them unsuccessfully, as you can see on the two other pictures. I finally had to invite the real expert — my grandson — to do it.



I used to hate crocheting. Now it's been growing on me.

To prepare for this magic trick, take all the spades out of a deck and place them in the following order: seven, ace, queen, two, eight, three, jack, four, nine, five, king, six, and ten. Turn the assembled deck face down, so that the seven is on top. Now you are ready to do the trick.
Magic trick. Transfer the top card to the bottom of your deck and deal the new top card face-up on the table. Repeat this process until all the cards are dealt. And — abracadabra — the cards are dealt in order.
I showed this trick to my grandchildren, and they decided to reproduce it. They tried to calculate where each card goes, without too much success. Then my son showed them another trick: how to arrange the cards without calculation. He started building his arranged deck from the end of the trick with all the cards in order face-up on the table with the king on top. He took the king and put it face-down into his hand. Then he repeated the following procedure until all the cards were in his hand: He took the next card from the table and put it face-down on top of the one in his hand. Then he moved the card from the bottom of his deck to the top. And — abracadabra — the cards are arranged correctly for the trick.
Next time, I should ask my grandkids to show this trick with the whole deck.


Each time I teach my students about the Möbius strip, I bring paper, scissors, and tape to class. The students make Möbius strips, and then I ask them to cut the strips in half along the midline and predict the result.
Then we move to advanced strips. To glue the Möbius strip, you need one turn of the paper. An interesting experiment is to glue strips with two, three, or more turns. In this case, too, it is fun to cut them along the midline and predict the shape of the resulting thingy. My class ends with a big paper mess.
As you might know, I am passionate about recycling. So I have always wanted to buy Möbius strips that can be cut in half and then put back together. I didn't find them, so I made them myself from zippers. Now I can unzip them along the midline and zip them back together. I hope to have less mess in my future classes. We'll see.
I recently posted my new favorite probability puzzle from the fall 2019 issue of Emissary, submitted by Peter Winkler.
Puzzle. Alice and Bob each have a biased coin that flips heads with probability 51% and 100 dollars to play with. The buzzer rings, and Alice and Bob begin flipping their coins once per minute and betting one dollar on each flip against the house. The bet is at even odds: each round, each of them either loses or wins a dollar. Alice always bets on heads, and poor Bob, always on tails. As it happens, however, both eventually go broke. Who is more likely to have gone broke first?
Follow-up question: They play the same game as above, but this time Alice and Bob are flipping the same coin (biased 51% toward heads). Again, assuming both eventually go broke, who is more likely to have lost their money first?
One might assume that Bob obviously got a bad deal. He will lose his money very fast. So the answer to both questions must be that Bob loses his money first. If you know me, you should realize that I wouldn't have given you this puzzle if the answer was that intuitive. I love counter-intuitive puzzles.
Bob has a disadvantage, so he is guaranteed to lose eventually. Alice has an advantage, so she might lose, or she might not. If she goes broke, that means there should be more tails in the flips than if she doesn't go broke. How does this influence the second scenario, in which they use the same coin? As we are expecting a lot of tails in the flips, the situation should be better for Bob as compared to the first scenario. Given that I posed this puzzle, one might decide that in the follow-up question Bob doesn't go broke first. Is it a tie?
But, if Bob is the first to go broke in the first scenario, why would I include the first part of the puzzle at all? If you know me, you should wonder what makes the first question interesting. Or maybe, you know Peter Winkler, in which case you should also wonder the same thing.
I gave you enough meta information to guess the amazing counter-intuitive answers to these two questions: in the first scenario, they tie; and in the second scenario, Alice goes broke first with higher probability.
To prove that they tie in the first scenario, let me first define a switch on a sequence of coin flips. A switch changes each head into tails and vice versa. The switch creates a one-to-one correspondence between the sequences of flips where Bob goes broke with the sequences where Alice goes broke. Suppose p is the probability that Alice goes broke with a particular sequence a, and q is the probability that Bob goes broke with a `switched' sequence b. Then p = rq, where r = (49/51)200. The reason is that sequence a has exactly 200 more tails than sequence b. The same ratio r works for any pair of switched sequences. Bob is guaranteed to go broke eventually. But to calculate the conditional probability of Alice going broke with sequence a, given that she does go broke, we need to divide the probability of the sequence a occurring by the probability that Alice goes broke. The resulting probability distribution on sequences of length n has to be the same as for Bob because it has to sum to one. If Alice goes broke, then the probability that she goes broke after n flips is the same as for Bob. That means they tie.
To answer the second question, we use the switch again. The switch creates a one-to-one correspondence between sequences of flips where Alice goes broke first and Bob second, and vice versa. The sequence for which Alice loses second has 200 more tails than the corresponding sequence where Bob loses second. Thus, in each pair of two switched sequences, the probability of the sequence where Alice loses second is equal to r times the probability of the sequence where Bob loses second. Thus, the probability of Alice winning is r times the probability of Bob winning, and r is a very small number.

Here are my newly-made Borromean rings: two identical sets of them. They are an example of three linked rings, with any two of them not linked. The top set is positioned the way the Borromean rings are usually presented. You can see that any two rings are not linked by mentally ignoring the third one. For example, the red ring is on top of the green one, the green one is on top of the blue one, and the blue one is on top of the red one. They have a non-transitive ordering.
The bottom set of rings is arranged for a lazier thinker. Obviously, the blue and green rings are not linked.
I used to be proud of my Russian math education. I am still proud of my high school one, but not so much of the one I received in college. In Soviet Russia, a student had to choose their major before applying to college. I wanted to study mathematics, and I got accepted to the best place for it in Soviet Russia: mekhmat — the math school at the Moscow State University. I used to be proud of my education there, but now I have my doubts.
I had to take, on average, four math classes per semester for five years, which totals about 40 math classes. Woo hoo! I don't think American students could even choose to take that many. This was presumably good, but most of the courses were required, and their curriculum remained unchanged for many, many years. Obviously, the system was very rigid. The faculty members feared retaliation from the communist party and forgot how to take initiative. The bureaucracy prevented the department from adding new and exciting math to the outdated curriculum.
This post is not about my grades but about the actual subjects that we were taught then. But, in case anyone is wondering, my only B was in English; everything else was straight As.
Some of the classes listed below lasted two or more semesters, that's why they do not sum up to the promised 40. Unfortunately, I do not remember which ones. These were the required math classes:
An impressive list? But guess what — I remember nothing from most of these classes. As an exception, I remember bits of Differential Equations, taught by Vladimir Arnold, a charismatic teacher. I remember Linear Algebra well, not because of my Linear Algebra class, but because I read Gelfand's book on the subject and loved it. I remember that the Differential Geometry and Topology class was taught by Fomenko with great pictures and boring material. By the time I took Fomenko's class, I already knew topology from an unofficial class taught by Dmitry Fuchs, which was so much better. In fact, in order to learn what I wanted, I had to take many classes unofficially, so my total is actually way above 40.
By junior year, we were finally allowed to choose some classes which would count towards our transcripts, and this is what I picked.
I remember these classes much more vividly. I also wrote a graduate thesis: "Models of Representations of Generalized Clifford Algebras." I loved working on that paper.
We had non-math classes too: everyone had to take them.
To graduate, everyone had to pass two state exams: Mathematics and Scientific Communism. Whatever the latter might mean.
Did I mention that I am no longer proud of my former Soviet college education? What a colossal waste of time!
Pete McCabe presented his trick, Persistimis Possessiamo, at the Gathering for Gardner in 2018.
Trick. Pete asked for two volunteers, let's call them Alice and Bob. Bob took out his favorite card, the Queen of Spades, from the deck and put it back following Pete's instructions. Then Alice dealt the deck alternatively into two piles, Bob's and hers, starting with Bob's. Alice took her pile and repeated the same process several times until only one card was left. And, abracadabra: it was Bob's chosen Queen of Spades.
Pete McCabe is interested in scripting magic. In his blog post, Scripting Magic for Zoom, he describes ways to make sure that Bob inserts his card into the 22nd place without using sleight of hand, but rather using a theatrical script which makes the process magical rather than mathematical. The magic part is related to the fact that the number of letters in the trick title, Persistimis Possessiamo, is 22. As a result, he can do the trick on Zoom without ever touching the cards.
Once a magician knows how to manipulate the volunteer to insert the card into a specific place in the deck, the trick becomes deterministic and works on any-sized deck, as long as the magician can calculate where the card goes. We will now perform this calculation.
We denote our card-inserting sequence as a(n), where n is the size of the deck, and a(n) is the place where the card is inserted. For starters, a(2n+1) = a(2n): when the size of the deck is odd, the last card during the first deal goes to Bob, and doesn't effect the other deals. Now, we obviously have a recursion. First, we observe that in order to end up in Alice's pile after the first deal, Bob's chosen card should occupy an even-numbered place. Suppose we start with 2n cards. After the first deal, Bob's chosen card is in the place number a(2n)/2 from the bottom in Alice's pile. That means, the card is in the place number n + 1 − a(2n)/2 from the top. This gives us an equation: a(n) = n + 1 − a(2n)/2, which is equivalent to a recursion: a(2n) = 2(n + 1 − a(n)).
Given that each element of the sequence a(n) is doubled, we are only interested in even-indexed values. Consider b(n) = a(2n) = a(2n+1). Then b(1) = 2, and the recursion for b is b(n) = 2(n + 1 − b⌊n/2⌋).
From here, we get the sequence, which is now sequence A350652 in the OEIS:
2, 2, 4, 6, 8, 6, 8, 6, 8, 6, 8, 14, 16, 14, 16, 22, 24, 22, 24, 30, 32, 30, 32, 22, 24, 22, 24, ... .
Here is a classical puzzle I often give to my students.
Puzzle. The sultan has three red hats and two blue ones. He wants to test his three wizards, who know his hat collection. He asks them to close their eyes and puts a hat on each of their heads. After the wizards open their eyes, they see each other's hats, but not their own. The sultan asks each of them to guess the color of their own hat, without communicating with each other. In this particular test, the sultan only puts red hats on the wizards' heads. Sometime after the wizards open their eyes, one of them guesses his hat's color. How did he guess?
Here is how my students explain the solution. If a wizard sees two blue hats, he immediately knows that his hat must be red. That means, if no one immediately announces their hat's color, at least two of them are wearing red hats. In this case, if a wizard sees one red hat, he knows that his hat must also be red. So such a wizard can guess the color of his hat. If after some more time, no one announces their hat color, all the hats worn must be red.
After the students solve the problem, I run an evil experiment on them. I show the students my two blue and three red hats and ask three volunteers to close their eyes. Then, I put two red hats and one blue hat on their heads, and the blue hat goes on the fastest thinker in the group. I did this experiment many times. Half the time, the fastest thinker overestimates how fast the other students think and guesses, mistakenly, that s/he is wearing the red hat. Gotcha!
After the experiment, we discuss what is really going on in this puzzle. This is how I start my class on common knowledge.

I plan to teach knot theory to my students. So, I made four blue knots which are actually the four simplest non-trivial knots. Then I made the red ones which are mirror images of the blue ones.
Then I fiddled with the figure-eight knots, which are the second ones from the left. Out of all these four types of knots, the figure-eight knot is the only one that is amphichiral: its mirror image is equivalent to itself. It was fun to physically transform the red one to look identical to the blue one. So, I decided to crochet another pair of figure-eight knots for my students to fiddle with.
Did I mention that I hate crocheting?
I grew up relatively poor, but I wasn't aware of it and didn't care. In 7th grade, I went to a new school for children gifted in math. Looking back, I realize that most of my classmates there were privileged. My first clue about my own financial disadvantages arrived when my math teacher, Inna Victorovna, offered me several of her old dresses. I do not remember what she said to me exactly, but I remember she was tactful, so much so that I felt comfortable taking the dresses.
In an instant, I was better dressed than I had ever been. I especially loved the brown dress which I wore for my first visit to Gelfand's seminar.
A few years passed; I went to college and married Andrey. Things got somewhat better financially, but I was still struggling. My mother-in-law, Veronika, was well-off and loved clothes. She had a habit of ordering a new dress from her tailor, every season, four times a year. In Soviet Russia, this was a lot of dresses.
One day, Veronika decided to give me some of her old dresses. Unlike my math teacher, she said something that I will never forget. She told me that she was getting rid of those dresses because they were out of fashion and made her look old. I was in my twenties at the time and didn't want to look old either. However, I didn't have much choice in clothes, so I wore the dresses. I hated them.

Here is a famous matchstick puzzle based on the given picture.
Puzzle. Can you move three matchsticks to turn the fish around?
Here is my bonus puzzle.
Bonus Puzzle. Can you turn the fish by moving two matchsticks?
I usually collect puzzles related to math after each MIT mystery hunt. I just discovered that I never reviewed the 2013 hunt, though I started writing the post. Plus, I knew the puzzles of that year better than other year's puzzles: I was on the writing team. Not to mention, the hunt had some real gems.
I start with mathematical puzzles:
Logic puzzles:
Computer science puzzles:
Crypto puzzles:
Word puzzles:
Misc puzzles:
Other puzzles I worked on:
Below, you can find a lovely problem from the 2016 All-Russian Olympiad suggested by Bogdanov and Knop. I took some liberties translating it.
Problem. King Hiero II of Syracuse has 11 identical-looking metallic ingots. The king knows that the weights of the ingots are equal to 1, 2, ..., 11 libras, in some order. He also has a bag, which would be ripped apart if someone were to put more than 11 libras worth of material into it. The king loves the bag and would kill if it was destroyed. Archimedes knows the weights of all the ingots. What is the smallest number of times he needs to use the bag to prove the weight of one of the ingots to the king?
And a bonus question from me.
Bonus. Add one more weighing to prove the weight of three more ingots.
Do you know that I participated in Linguistics Olympiads in high school? They are not well-known in the US, but the Soviet Union has been running them since 1965. The first International Linguistics Olympiad was conducted in 2003, and the US joined in 2007. They are called Computational Linguistics because you are expected to discover some phenomenon in an unfamiliar language on the fly instead of knowing a lot of languages already. The problems mostly need logic and are a good fit for a person who likes mathematics. However, a feel for languages is very helpful.
I do not remember why I started attending the Olympiads, but I remember that there were two sets of problems: more difficult for senior and less difficult for non-senior years. I used to be really good at these Olympiads. When I was in 8th grade, I finished my problems before the time ran out and started the senior problems. I got two awards: first place for non-senior years and second place for senior years. In 9th grade, I got two first-place awards. I didn't know what to do in 10th grade, which was a senior year at that time in the USSR. I couldn't get two first-place awards, as I could no longer compete in the non-senior category. I felt ashamed that my result could only be worse than in the previous years, so I just didn't go.

The prizes were terrific: they gave me tons of rare language books. In the picture, a guy from the jury is carrying my prizes for me. I immediately sold the books at used-books stores for a good price. Looking back, I should have gone to the Olympiad in 10th grade: my winter boots had big holes.

What do you give a mathematician who likes only mathematics if you want to expand her geographical horizon? I just got such a gift: A math book that made me feel that I was in Australia. The book, A Dingo Ate My Math Book: Mathematics from Down Under, written by Burkard Polster and Marty Ross, has lovely essays, nice pictures, and a strong Australian flavor.
Last revised December 2023