A quadrilateral is given in space, such that its edges are tangent to a sphere. Prove that all the points of tangency lie in one plane.
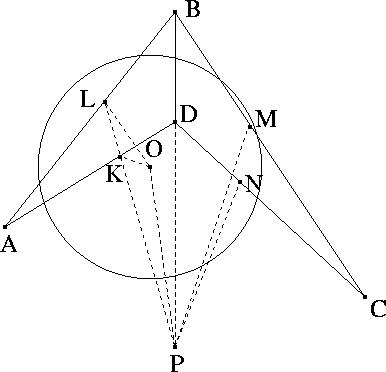
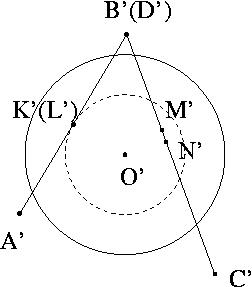
Let ABCD be the given quadrilateral, let KLMN be the points where it is tangent to the shpere, and let the shpere have center O (see Figure 1). The points KLBD are coplanar (because of A). Let us assume for now that the lines KL and BD intersect at a point P. Let us consider the central projection of this structure from P onto a plane perpendicular to OP (see Figure 2). The projections of the points K and L, as well as B and D, coincide, by the choice of the point P. Now, the dashed circle is the projection of the intersection of the shpere with the plane perpendicular to OP passing through K (which coincides with the projection of the corresponding structure through L). Since AD was tangent to the shpere, A'D' is tangent to the dashed circle, so O'K' is perpendicular to A'D'. Now the punchline --- the same argument shows that O'N' and O'M' are both perpendicular to C'D'! Therefore M' and N' coincide, so M and N are on the same ray from P. Conclusion: KL and MN intersect (at P), so KLMN are coplanar. The same argument works in the degenerate case when KL and BD are parallel by considering an orthogonal projection onto a plane perpendicular to BD. In that case, KL and MN are parallel.
 |
 |
| Figure 1 | Figure 2 |
Last revised August 2003